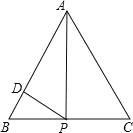
【题目】(2016山东省泰安市第20题)如图,正△ABC的边长为4,点P为BC边上的任意一点(不与点B、C重合),且∠APD=60°,PD交AB于点D.设BP=x,BD=y,则y关于x的函数图象大致是( )
A.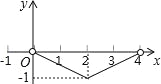 B.
B.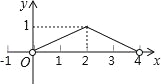
C.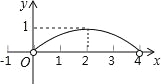 D.
D.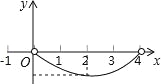
参考答案:
【答案】C
【解析】
试题分析:由△ABC是正三角形,∠APD=60°,可证得△BPD∽△CAP,然后由相似三角形的对应边成比例,即可求得答案.∵△ABC是正三角形,∴∠B=∠C=60°,∵∠BPD+∠APD=∠C+∠CAP,∠APD=60°,
∴∠BPD=∠CAP,∴△BPD∽△CAP,∴BP:AC=BD:PC,
∵正△ABC的边长为4,BP=x,BD=y,∴x:4=y:(4﹣x), ∴y=-![]() +x.
+x.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)某校为美化校园,计划对面积为1800m2的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且在独立完成面积为400m2区域的绿化时,甲队比乙队少用4天.
(1)求甲、乙两工程队每天能完成绿化的面积分别是多少m2?
(2)若学校每天需付给甲队的绿化费用为0.4万元,乙队为0.25万元,要使这次的绿化总费用不超过8万元,至少应安排甲队工作多少天?
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(﹣3x)2(x﹣3y)
(2)(12a3﹣6a2+3a)÷3a
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:
(1)a3b﹣ab;
(2)(a﹣b)2﹣6(a﹣b)+9.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
已知n边形的内角和θ=(n-2)×180°.
(1)甲同学说,θ能取360°;而乙同学说,θ也能取630°.甲、乙的说法对吗?若对,求出边数n.若不对,说明理由;
(2)若n边形变为(n+x)边形,发现内角和增加了360°,用列方程的方法确定x.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若二次函数y=kx2﹣4x+1的图象与x轴有交点,则k的取值范围是( )
A. k≤4 B. k≥4 C. k>4且k≠0 D. k≤4且k≠0
-
科目: 来源: 题型:
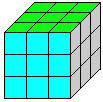
查看答案和解析>>【题目】如图,是一个我们喜欢玩的魔方,它是由若干个小正方体组成的一个大正方体,在这个大正方体的六个面上,分别涂有6种不同的颜色.根据你的观察与想象回答下列问题:①有几个小正方体只有一个面被涂有颜色?②有几个小正方体有两个面被涂有颜色?③有几个小正方体有三个面被涂有颜色?
相关试题

