【题目】如图,在平面直角坐标系内,点A的坐标为(0,24),经过原点的直线l1与经过点A的直线l2相交于点B,点B的坐标为(18,6).
(1)求直线l1,l2对应的函数表达式;
(2)点C为线段OB上一动点(点C不与点O,B重合),作CD∥y轴交直线l2于点D,设点C的纵坐标为a,求点D的坐标(用含a的代数式表示).
参考答案:
【答案】(1) y=-x+24;(2) D的坐标为(3a,-3a+24)
【解析】
(1)根据题意可设直线l1的表达式为y=k1x,设直线l2的表达式为y=k2x+b,将点B、点A的坐标代入直线表达式中求出系数,则可得直线表达式;
(2) 因为点C在直线l1上,已知点C的纵坐标,由直线表达式可得点C的横坐标,因为CD//y轴,所以点D的横坐标与点C的横坐标相等,将D点横坐标代入l2表达式,即可得点D的坐标.
(1)设直线l1对应的函数表达式为y=k1x,由它过点(18,6)得18k1=6,解得k1=![]()
所以直线l1对应的函数表达式为y=![]() x;
x;
设直线l2对应的函数表达式为y=k2x+b,由它过点A(0,24),B(18,6)得b=24,18k2+b=6,解得k2=-1,所以直线l2对应的函数表达式为y=-x+24.
(2)因为点C在直线l1上,且点C的纵坐标为a,所以a=![]() x.
x.
所以x=3a,故点C的坐标为(3a,a).
因为CD∥y轴,
所以点D的横坐标为3a.
因为点D在直线l2上,
所以点D的纵坐标为-3a+24.
所以点D的坐标为(3a,-3a+24).
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有甲、乙两个瓷器店出售茶壶和茶杯,茶壶每只价格为20元,茶杯每只价格为5元,已知甲店制定的优惠方法是买一只茶壶送一只茶杯,乙店按总价的92%付款.学校办公室需要购买茶壶4只,茶杯若干只(不少于4只).
(1)当购买多少只茶杯时,两店的优惠方法付款一样多?
(2)当需要购买40只茶杯时,若让你去办这件事,你打算去哪家商店购买?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示已知
 ,
,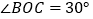 ,OM平分
,OM平分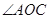 ,ON平分
,ON平分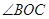 ;
;(1)
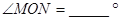 ;
;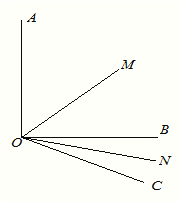
(2)如图∠AOB=900,将OC绕O点向下旋转,使∠BOC=
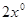 ,仍然分别作∠AOC,∠BOC的平分线OM,ON,能否求出∠MON的度数,若能,求出其值,若不能,试说明理由.
,仍然分别作∠AOC,∠BOC的平分线OM,ON,能否求出∠MON的度数,若能,求出其值,若不能,试说明理由.
(3)
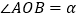 ,
,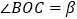 ,仍然分别作∠AOC,∠BOC的平分线OM,ON,能否求出∠MON的度数,若能,求
,仍然分别作∠AOC,∠BOC的平分线OM,ON,能否求出∠MON的度数,若能,求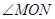 的度数;并从你的求解中看出什么什么规律吗?
的度数;并从你的求解中看出什么什么规律吗?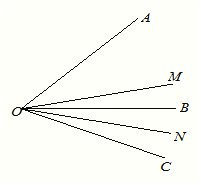
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,函数y=2x和y=﹣x的图象分别为直线l1 , l2 , 过点(1,0)作x轴的垂线交l1于点A1 , 过点A1作y轴的垂线交l2于点A2 , 过点A2作x轴的垂线交l1于点A3 , 过点A3作y轴的垂线交l2于点A4 , …依次进行下去,则点A2017的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:线段AB=20cm.
(1)如图1:点P沿线段AB自A点向B点以2厘米/秒运动,点P出发2秒后,点Q沿线段BA自B点向A点以3厘米/秒运动,问再经过几秒后P、Q相距5cm?

(2)如图2:
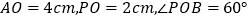 ,点P绕着点O以60度/秒的速度逆时针旋转一周停止,同时点Q沿直线BA自B点向A点运动,假若点P、Q两点能相遇,求点Q运动的速度 .
,点P绕着点O以60度/秒的速度逆时针旋转一周停止,同时点Q沿直线BA自B点向A点运动,假若点P、Q两点能相遇,求点Q运动的速度 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(1)-3+5;
(2)-3-2;
(3)
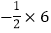 ;
; (4)
 ;
;(5)
 ;
; (6)
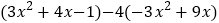 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】杨洋计划将今年春节期间得到的压岁钱的一部分作为自己一年内购买课外书籍的费用,其余的钱计划买些玩具去看望市福利院的孩子们.某周日杨洋在商店选中了一种小熊玩具,单价是10元,按原计划买了若干个,结果他的压岁钱还余30%,于是杨洋又多买了6个小熊玩具,这样余下的钱仅是压岁钱的10%.问杨洋原计划买几个小熊玩具,杨洋的压岁钱共有多少元?
相关试题

