【题目】如图,在平面直角坐标系中,已知矩形AOBC的顶点C的坐标是(2,4),动点P从点A出发,沿线段AO向终点O运动,同时动点Q从点B出发,沿线段BC向终点C运动.点P、Q的运动速度均为1个单位,运动时间为t秒.过点P作PE⊥AO交AB于点E.
(1)求直线AB的解析式;
(2)设△PEQ的面积为S,求S与t时间的函数关系,并指出自变量t的取值范围;
(3)在动点P、Q运动的过程中,点H是矩形AOBC内(包括边界)一点,且以B、Q、E、H为顶点的四边形是菱形,直接写出t值和与其对应的点H的坐标.

参考答案:
【答案】(1)直线AB的解析式为y=﹣2x+4.(2)S![]() t2﹣t(2<t≤4).(3)t1=
t2﹣t(2<t≤4).(3)t1=![]() ,H1(
,H1(![]() ),t2=20﹣
),t2=20﹣![]() ,H2(10﹣
,H2(10﹣![]() ,4).
,4).
【解析】试题分析:(1)根据待定系数法即可得到;
(2)过点Q作QF//x轴交y轴于点F,有两种情况:当0<t<2时,PF=4﹣2t,当2<t≤4时,PF=2t﹣4,然后根据面积公式即可求得;
(3)由菱形的邻边相等即可得到.
试题解析:(1)∵C(2,4),
∴A(0,4),B(2,0),
设直线AB的解析式为y=kx+b,
∴![]() ,
,
解得![]()
∴直线AB的解析式为y=﹣2x+4.
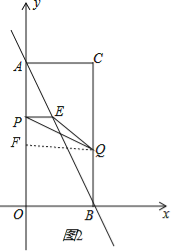
(2)如图2,过点Q作QF⊥y轴于F,
∵PE//OB,
∴![]()
∴有AP=BQ=t,PE=![]() t,AF=CQ=4﹣t,
t,AF=CQ=4﹣t,
当0<t<2时,PF=4﹣2t,
∴S=![]() PEPF=
PEPF=![]() ×
×![]() t(4﹣2t)=t﹣
t(4﹣2t)=t﹣![]() t2,
t2,
即S=﹣![]() t2+t(0<t<2),
t2+t(0<t<2),
当2<t≤4时,PF=2t﹣4,
∴S=![]() PEPF=
PEPF=![]() ×
×![]() t(2t﹣4)=
t(2t﹣4)=![]() t2﹣t(2<t≤4).
t2﹣t(2<t≤4).
(3)t1=![]() ,H1(
,H1(![]() ,
,![]() ),
),
t2=20﹣8![]() ,H2(10﹣4
,H2(10﹣4![]() ,4).
,4).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,直线y=-2x+1与y轴交于点C,直线y=x+k(k≠0)与y轴交于点A,与直线y=-2x+1交于点B,设点B的横坐标为x0.
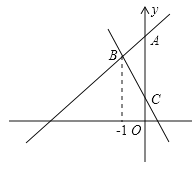
(1)如图,若x0=-1.
①求点B的坐标及k的值;
②求直线y=-2x+1、直线y=x+k与y轴所围成的△ABC的面积;
(2)若-2<x0<-1,求整数k的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=2x+b.
(1)它的图像与两坐标轴所围成的图形的面积等于4,求b的值;
(2)它的图像经过一次函数y=-2x+1、y=x+4图像的交点,求b的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店销售A型和B型两种电脑,其中A型电脑每台的利润为400元,B型电脑每台的利润为500元.该商店计划再一次性购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
(1)求y关于x的函数关系式;
(2)该商店购进A型、B型电脑各多少台,才能使销售总利润最大,最大利润是多少?
(3)实际进货时,厂家对A型电脑出厂价下调a(0<a<200)元,且限定商店最多购进A型电脑60台,若商店保持同种电脑的售价不变,请你根据以上信息,设计出使这100台电脑销售总利润最大的进货方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两人轮流在黑板上写下不超过
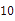 的正整数(每次只能写一个数),规定禁止在黑板上写已经写过的数的约数,最后不能写的为失败者,如果甲写第一个,那么,甲写数字( )时有必胜的策略.
的正整数(每次只能写一个数),规定禁止在黑板上写已经写过的数的约数,最后不能写的为失败者,如果甲写第一个,那么,甲写数字( )时有必胜的策略.A. 10 B. 9 C. 8D.6
-
科目: 来源: 题型:
查看答案和解析>>【题目】若直线
 经过点
经过点 ,直线
,直线 经过点
经过点 ,且
,且 与
与 关于
关于 轴对称,则
轴对称,则 与
与 的交点坐标为( )
的交点坐标为( )A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲.乙两种商品原来的单价和为100元,因市场变化,甲商品降价10%,乙商品提价40%,调价后两种商品的单价和比原来的单价和提高了20%.若设甲.乙两种商品原来的单价分别为x元.y元,则可列方程组为_________________;
相关试题

