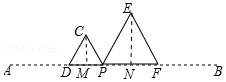
【题目】已知:点P为线段AB上的动点(与A、B两点不重合),在同一平面内,把线段AP、BP分别折成等边△CDP和△EFP,且D、P、F三点共线,如图所示. 
(1)若DF=2,求AB的长;
(2)若AB=18时,等边△CDP和△EFP的面积之和是否有最大值,如果有最大值,求最大值及此时P点位置,若没有最大值,说明理由.
参考答案:
【答案】
(1)解:∵△CDP和△EFP是等边三角形,
∴CD=PC=PD,EF=EP=PF,AP=3PD,BP=3PF,
∵DF=PD+PF=2,
∴AB=AP+BP=3DF=3×2=6
(2)解:没有最大值,理由如下:
设CD=PC=PD=x,则EF=EP=PF= ![]() (18﹣3x)=6﹣x,
(18﹣3x)=6﹣x,
作CM⊥PD于M,EN⊥PF于N,
则DM= ![]() PD=
PD= ![]() x,PN=
x,PN= ![]() PF=
PF= ![]() (6﹣x),
(6﹣x),
∴CM= ![]() DM=
DM= ![]() x,EN=
x,EN= ![]() (6﹣x),
(6﹣x),
∴△CDP的面积= ![]() PDCM=
PDCM= ![]() x2,△EFP的面积=
x2,△EFP的面积= ![]() (6﹣x)2,
(6﹣x)2,
∴等边△CDP和△EFP的面积之和S= ![]() x2+
x2+ ![]() (6﹣x)2=
(6﹣x)2= ![]() x2﹣3
x2﹣3 ![]() x+9
x+9 ![]() ,
,
∵ ![]() >0,
>0,
∴S有最小值,没有最大值.
【解析】(1)由等边三角形的性质容易得出结果;(2)设CD=PC=PD=x,则EF=EP=PF=6﹣x,求出等边△CDP和△EFP的面积之和S= ![]() x2﹣3
x2﹣3 ![]() x+9
x+9 ![]() ,
, ![]() >0,得出S有最小值,没有最大值.
>0,得出S有最小值,没有最大值.
【考点精析】认真审题,首先需要了解二次函数的最值(如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a),还要掌握等边三角形的性质(等边三角形的三个角都相等并且每个角都是60°)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名同学进行登山比赛,图中表示甲、乙两人沿相同的路线同时从山脚出发,各自离山脚的距离随时间变化的图象,根据图象中的有关数据回答下列问题:
(1)分别求出表示甲、乙两同学登山过程中离山脚的距离h(千米)与时间t(时)的函数表达式;
(2)当甲到达山顶时,乙行进到山路上的某点A处,求A点距山顶的距离;
(3)在(2)的条件下,设乙同学从A点继续登山,甲同学到达山顶后游玩
 小时,沿原路下山,在点B处与乙同学相遇,此时点B与山顶距离为1千米,相遇后甲、乙各自沿原路下山和上山,求乙到达山顶时,甲离山脚的距离是多少千米?
小时,沿原路下山,在点B处与乙同学相遇,此时点B与山顶距离为1千米,相遇后甲、乙各自沿原路下山和上山,求乙到达山顶时,甲离山脚的距离是多少千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣
 x2+bx+c与y轴交于点C,与x轴交于A、B两点(点A在原点左侧,点B在原点右侧),且∠ACB=90°,tan∠BAC=
x2+bx+c与y轴交于点C,与x轴交于A、B两点(点A在原点左侧,点B在原点右侧),且∠ACB=90°,tan∠BAC=  . ①求抛物线的解析式;
. ①求抛物线的解析式;
②若抛物线顶点为P,求四边形APCB的面积.
-
科目: 来源: 题型:
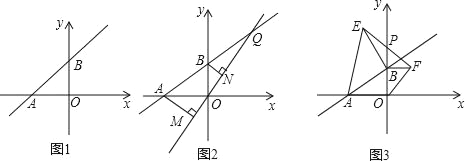
查看答案和解析>>【题目】如图1,直线l:y=mx+10m与x轴负半轴、y轴正半轴分别交于A、B两点.
(1)当OA=OB时,试确定直线l的函数表达式;
(2)在(1)的条件下,如图2,设Q为直线AB上一点,作直线OQ,过A、B两点分别作AM⊥OQ于M,BN⊥OQ于N,若AM=8,BN=6,求MN的长;
(3)当m取不同的值时,点B在y轴正半轴上运动,分别以OB、AB为边,点B为直角顶点在第一、二象限内作等腰直角△OBF和等腰直角△ABE,连EF交y轴于P点,如图3.问:当点B在 y轴正半轴上运动时,试猜想PB的长是否为定值?若是,请求出其值;若不是,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读以下材料:
高斯是德国著名的大科学家,他最出名的故事就是在他10岁时,小学老师出了一道算术难题:计算1+2+3+……+100=?
在其他同学还在犯难时,却很快传来了高斯的声音:“老师,我已经算好了!”
老师很吃惊,高斯解释道:因为1+100=101,2+99=101,3+98=101,……,49+52=101,50+51=101,而像这样的等于101的组合一共有50组,所以答案很快就可以求出:101×50=5050。
根据以上的信息,请同学们:
(1)计算1+3+5+7+…+99的值.
(2)计算2+4+6+8+…+200的值.
(3)用含a和n的式子表示运算结果:求a+2a+3a+…+na的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列解题过程:(-15)÷(
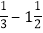 -3)×6
-3)×6(解析)原式=(-15)÷(-
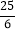 )×6 (第一步)
)×6 (第一步)=(-15)÷(-25)(第二步)
=-
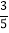 (第三步)
(第三步)解答问题:
①上面解答过程有两个错误,第一处是第______步,错误的原因是______;第二处是第______步,错误的原因是______;
②请你正确解答本题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】材料:
一般地,n个相同的因数a相乘:
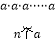 记为
记为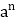 .如23=8,此时,3叫做以2为底8的对数,记为log28(即log28=3).
.如23=8,此时,3叫做以2为底8的对数,记为log28(即log28=3).一般地,若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为logab(即logab=n).如34=81,则4叫做以3为底81的对数,记为log381(即log381=4).
问题:
(1)计算以下各对数的值:log24=______,log216=______,log264=______.
(2)观察(1)中三数4、16、64之间满足怎样的关系式为______log24、log216、log264之间又满足怎样的关系式:______
(3)由(2)的结果,你能归纳出一个一般性的结论吗?logaM+logaN=______(a>o且a≠1,M>0,N>0).
相关试题

