【题目】完成推理填空:如图在△ABC中,已知∠1+∠2=180°,∠3=∠B,试说明∠AED=∠C.
解:∵∠1+∠2=180°( ), +∠EFD=180°(邻补角定义),
∴ (同角的补角相等)
∴AB∥ (内错角相等,两直线平行)
∴∠ADE=∠3( )
∵∠3=∠B(已知)∴ (等量代换)
∴ ∥BC(同位角相等,两直线平行)
∴∠AED=∠C( )

参考答案:
【答案】已知 ∠1 ∠2=∠EFD EF 两直线平行内错角相等 ∠ADE=∠3 DE 两直线平行同位角相等
【解析】
首先根据∠1+∠EFD=180°和∠1+∠2=180°可以证明∠EFD=∠2,再根据内错角相等,两直线平行可得AB∥EF,进而得到∠ADE=∠3,再结合条件∠3=∠B可得∠ADE=∠B,进而得到DE∥BC,再由平行线的性质可得∠AED=∠C.
∵∠1+∠2=180°(已知 ),∠1+∠EFD=180°(邻补角定义),
∴∠2=∠EFD(同角的补角相等)
∴AB∥EF(内错角相等,两直线平行)
∴∠ADE=∠3(两直线平行内错角相等)
∵∠3=∠B(已知)∴∠ADE=∠3(等量代换)
∴DE∥BC(同位角相等,两直线平行)
∴∠AED=∠C( 两直线平行同位角相等).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在矩形ABCD中,AB=a,BC=b,点E是线段AD边上的任意一点(不含端点A、D),连接BE、CE.
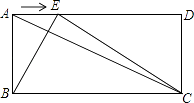
若a=5,sin∠ACB= ,解答下列问题:
,解答下列问题:
(1)填空:b=;
(2)当BE⊥AC时,求出此时AE的长;
(3)设AE=x,试探索点E在线段AD上运动过程中,使得△ABE与△BCE相似时,请写x、a、b三者的关系式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O△ABC的三条边所得的弦长相等,则下列说法正确的是( )
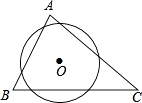
A.点O是△ABC的内心
B.点O是△ABC的外心
C.△ABC是正三角形
D.△ABC是等腰三角形 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:
(1)若点(x1 , y1),(x2 , y2)在图象上,当x2>x1>0时,y2>y1;
(2)当x<﹣1时,y>0;
(3)4a+2b+c>0;
(4)x=3是关于x方程ax2+bx+c=0的一个根,其中正确的个数为( )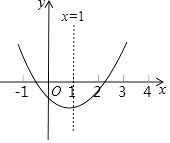
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,AD⊥BC,AE平分∠BAC交BC于点E.
(1)若∠B=20°,∠C=80°,求∠EAC和∠EAD的大小.
(2)若∠C>∠B,由(1)的计算结果,你能发现∠EAD与∠C﹣∠B的数量关系吗?写出这个关系式,并加以证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为1的正五边形ABCDE,顶点A、B在半径为1的圆上,其它各点在圆内,将正五边形ABCDE绕点A逆时针旋转,当点E第一次落在圆上时,则点C转过的度数为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某地一座抛物线形拱桥,桥拱在竖直平面内,与水平桥面相交于A、B两点,拱桥最高点C到AB的距离为4m,AB=12m,D、E为拱桥底部的两点,且DE∥AB,点E到直线AB的距离为5m,则DE的长为m.

相关试题

