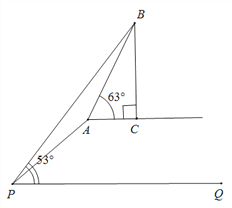
【题目】如图,坡度为1:2的斜坡AP的坡顶有一铁塔BC,在坡底P处测得塔顶B的仰角为53°,在沿斜坡前进![]() 米至A处,测得塔顶B的仰角为63°,已知A、C在同一水平面上.求铁塔BC的高度.
米至A处,测得塔顶B的仰角为63°,已知A、C在同一水平面上.求铁塔BC的高度.
(参考数据:sin63°≈0.89,cos63°≈0.45,tan63°≈2,sin53°≈0.8,cos53°≈0.6,tan53°≈![]() )
)
参考答案:
【答案】铁塔BC的高度约为25米
【解析】分析:作AD⊥PQ,垂足为D,延长BC交PQ于E,根据Rt△APD得出AD=5,PD=10,设BC的高度为x m,根据Rt△ACB的性质得出AC=![]() ,根据Rt△BPE的性质得出PE=
,根据Rt△BPE的性质得出PE=![]() ,然后根据PE-AC=10求出答案.
,然后根据PE-AC=10求出答案.
详解:解:作AD⊥PQ,垂足为D,延长BC交PQ于E,
在Rt△APD中AP=![]() ,坡度为1:2, 得AD=5,PD=10,
,坡度为1:2, 得AD=5,PD=10,
在矩形ADEC中,CE=AD=5,AC=DE,设BC的高度为x m,
在Rt△ACB中,tan63°=![]() , ∴AC=
, ∴AC=![]() ,
,
在Rt△BPE中,tan53°=![]() , ∴PE=
, ∴PE=![]() , ∴
, ∴![]() -
-![]() =10, 解得x=25.
=10, 解得x=25.
答:铁塔BC的高度约为25米
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列
 个生产、生活现象中,可用“两点之间线段最短”来解释的是( )
个生产、生活现象中,可用“两点之间线段最短”来解释的是( )A.用两根钉子就可以把木条固定在墙上
B.植树时,只要选出两棵树的位置,就能确定同一行树所在的直线
C.把弯曲的公路改直,就能缩短路程
D.砌墙时,经常在两个墙角的位置分别插一根木桩拉一条直的参照线
-
科目: 来源: 题型:
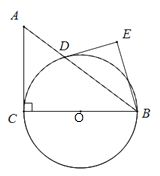
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以边BC为直径作⊙O,交AB于D,DE是⊙O的切线,过点B作DE的垂线,垂足为E.
(1)求证∠ABC=∠ABE;
(2)求DE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠BAC=100°,∠ABC=∠ACB,点D在直线BC上运动(不与点B、C重合),点E在射线AC上运动,且∠ADE=∠AED,设∠DAC=n.
(1)如图(1),当点D在边BC上时,且n=36°,则∠BAD= _________,∠CDE= _________.
(2)如图(2),当点D运动到点B的左侧时,其他条件不变,请猜想∠BAD和∠CDE的数量关系,并说明理由.
(3)当点D运动到点C的右侧时,其他条件不变,∠BAD和∠CDE还满足(2)中的数量关系吗?请画出图形,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:顶点、开口大小相同,开口方向相反的两个二次函数互为“反簇二次函数”.
(1)已知二次函数y=﹣(x﹣2)2+3,则它的“反簇二次函数”是__________________;
(2)已知关于x的二次函数y1=2x2﹣2mx+m+1和y2=ax2+bx+c,其中y1的图像经过点(1,1).若y1+y2与y1互为“反簇二次函数”.求函数y2的表达式,并直接写出当0≤x≤3时,y2的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(重温旧知)圆内接四边形的内角具有特殊的性质.
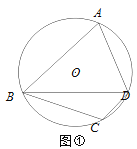
如图①,四边形ABCD是⊙O的内接四边形,若AB=BD,∠ABD=50°,则∠BCD=_______°.
(提出问题)圆内接四边形的边会有特殊性质吗?
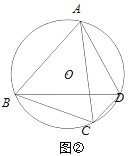
如图②,某数学兴趣小组进行深入研究发现:ABCD+BCDA=ACBD,请按他们的思路继续完成证明.
证明:如图③,作∠BAE=∠CAD,交BD于点E.
∵∠BAE=∠CAD,∠ABD=∠ACD,
∴△ABE∽△ACD,
∴
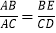 即ABCD=ACBE
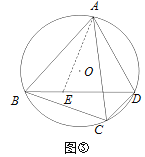
即ABCD=ACBE(应用迁移)如图,已知等边△ABC外接圆⊙O,点P为
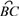 上一点,且PB=
上一点,且PB=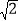 ,PC=1,求PA的长.
,PC=1,求PA的长.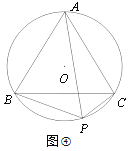
-
科目: 来源: 题型:
查看答案和解析>>【题目】下表是某中学足球冠军杯第一阶段
 组赛不完整的积分表.
组赛不完整的积分表. 组共
组共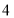 个队,每个队分别与其它
个队,每个队分别与其它 个队进行主客场比赛各一场,即每个队都要进行
个队进行主客场比赛各一场,即每个队都要进行 场比赛.每队每场比赛积分都是自然数.(总积分
场比赛.每队每场比赛积分都是自然数.(总积分 胜场积分
胜场积分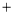 平场积分
平场积分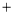 负场积分)
负场积分)球队
比赛场次
胜场次数
平场次数
负场次数
总积分
战神队




旋风队



龙虎队




梦之队


本次足球小组赛中,平一场积___________分,梦之队总积分是___________分.
相关试题

