【题目】下表是某中学足球冠军杯第一阶段![]() 组赛不完整的积分表.
组赛不完整的积分表.![]() 组共
组共![]() 个队,每个队分别与其它
个队,每个队分别与其它![]() 个队进行主客场比赛各一场,即每个队都要进行
个队进行主客场比赛各一场,即每个队都要进行![]() 场比赛.每队每场比赛积分都是自然数.(总积分
场比赛.每队每场比赛积分都是自然数.(总积分![]() 胜场积分
胜场积分![]() 平场积分
平场积分![]() 负场积分)
负场积分)
球队 | 比赛场次 | 胜场次数 | 平场次数 | 负场次数 | 总积分 |
战神队 |
|
|
|
|
|
旋风队 |
|
|
| ||
龙虎队 |
|
|
|
|
|
梦之队 |
|
|
本次足球小组赛中,平一场积___________分,梦之队总积分是___________分.
参考答案:
【答案】1 0
【解析】
根据旋风队平两场积2分即可得出平一场的分数,然后根据战神队和龙虎队的成绩得出负一场的分数即可求梦之队的总分.
∵旋风队平两场积2分
∴平一场积1分
对比战神队和龙虎队的成绩发现,胜一场比平一场多积2分,所以胜一场积3分,
设负一场得x分,则有
![]()
解得![]()
∴负一场积0分
因为梦之队负两场,所以积0分
故答案为:1;0.
-
科目: 来源: 题型:
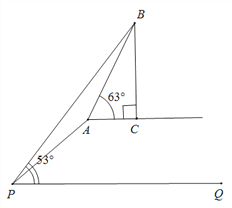
查看答案和解析>>【题目】如图,坡度为1:2的斜坡AP的坡顶有一铁塔BC,在坡底P处测得塔顶B的仰角为53°,在沿斜坡前进
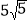 米至A处,测得塔顶B的仰角为63°,已知A、C在同一水平面上.求铁塔BC的高度.
米至A处,测得塔顶B的仰角为63°,已知A、C在同一水平面上.求铁塔BC的高度.(参考数据:sin63°≈0.89,cos63°≈0.45,tan63°≈2,sin53°≈0.8,cos53°≈0.6,tan53°≈
 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:顶点、开口大小相同,开口方向相反的两个二次函数互为“反簇二次函数”.
(1)已知二次函数y=﹣(x﹣2)2+3,则它的“反簇二次函数”是__________________;
(2)已知关于x的二次函数y1=2x2﹣2mx+m+1和y2=ax2+bx+c,其中y1的图像经过点(1,1).若y1+y2与y1互为“反簇二次函数”.求函数y2的表达式,并直接写出当0≤x≤3时,y2的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(重温旧知)圆内接四边形的内角具有特殊的性质.
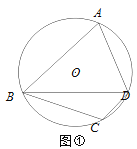
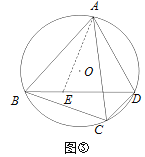
如图①,四边形ABCD是⊙O的内接四边形,若AB=BD,∠ABD=50°,则∠BCD=_______°.
(提出问题)圆内接四边形的边会有特殊性质吗?
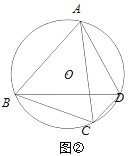
如图②,某数学兴趣小组进行深入研究发现:ABCD+BCDA=ACBD,请按他们的思路继续完成证明.
证明:如图③,作∠BAE=∠CAD,交BD于点E.
∵∠BAE=∠CAD,∠ABD=∠ACD,
∴△ABE∽△ACD,
∴
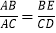 即ABCD=ACBE
即ABCD=ACBE(应用迁移)如图,已知等边△ABC外接圆⊙O,点P为
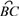 上一点,且PB=
上一点,且PB=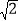 ,PC=1,求PA的长.
,PC=1,求PA的长.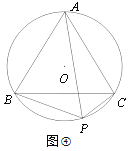
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC在平面直角坐标系xOy中的位置如图所示.

(1)作△ABC关于点C成中心对称的△A1B1C1.
(2)将△A1B1C1向右平移4个单位,作出平移后的△A2B2C2.
(3)在x轴上求作一点P,使PA1+PC2的值最小,并写出点P的坐标(不写解答过程,直接写出结果)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1、图2,△AOB,△COD均是等腰直角三角形,∠AOB=∠COD=90°,
(1)在图1中,AC与BD相等吗?请说明理由;
(2)若△COD绕点O顺时针旋转一定角度后,到达图2的位置,请问AC与BD还相等吗?为什么?
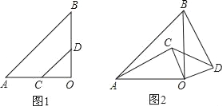
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市从
 年
年 月
月 日开始实施阶梯电价制,居民生活用电价格方案如下:
日开始实施阶梯电价制,居民生活用电价格方案如下:档次
月用电量
电价
(单位:元
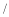 度)
度)春秋季(
 ,
,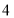 ,
,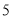 ,
,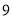 ,
,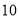 ,
,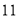 月)
月)冬夏季(
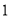 ,
,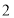 ,
,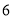 ,
,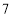 ,
,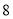 ,
,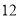 月)
月)第
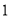 档
档不超过
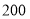 度的部分
度的部分不超过
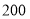 度的部分
度的部分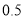
第
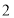 档
档超过
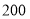 度但不超过
度但不超过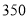 度的部分
度的部分超过
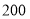 度但不超过
度但不超过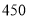 度的部分
度的部分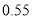
第
 档
档超过
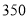 度的部分
度的部分超过
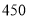 度的部分
度的部分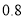
例:若某用户
 年
年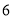 月的用电量为
月的用电量为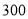 度,则需交电费为:
度,则需交电费为: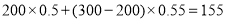 (元).
(元).(1)若小辰家
 年
年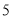 月的用电量为
月的用电量为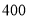 度,则需交电费多少元?
度,则需交电费多少元?(2)若小辰家
 年
年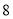 月和
月和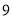 月用电量相同,共交电费
月用电量相同,共交电费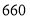 元,问小辰家
元,问小辰家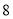 月份用多少度电?
月份用多少度电?
相关试题

