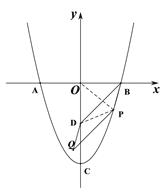
【题目】抛物线y=ax2+c与x轴交于A、B两点(A在B的左边),与y轴交于点C,抛物线上有一动点P
(1)若A(﹣2,0),C(0,﹣4)
①求抛物线的解析式;
②在①的情况下,若点P在第四象限运动,点D(0,﹣2),以BD、BP为邻边作平行四边形BDQP,求平行四边形BDQP面积的取值范围.
(2)若点P在第一象限运动,且a<0,连接AP、BP分别交y轴于点E、F,则问![]() 是否与a,c有关?若有关,用a,c表示该比值;若无关,求出该比值.
是否与a,c有关?若有关,用a,c表示该比值;若无关,求出该比值.
参考答案:
【答案】(1)①抛物线解析式为y=x2﹣4;②0<S四边形BDQP≤![]() ;(2)
;(2)![]() 的值与a,c无关,比值为1.
的值与a,c无关,比值为1.
【解析】试题分析:(1)①把 A(-2,0),C(0,-4)代入![]() ,求得a、c的值,即可得抛物线的解析式;②连接DB、OP,设P(
,求得a、c的值,即可得抛物线的解析式;②连接DB、OP,设P(![]() ,
, ![]() ),因A(-2,0),对称轴为
),因A(-2,0),对称轴为![]() 轴,可得B(2,0),即可得
轴,可得B(2,0),即可得![]()
![]()
![]() ,再由点P在第四象限运动,可得x单位取值范围
,再由点P在第四象限运动,可得x单位取值范围![]() ,由抛物线的图象即可得△BDP的取值范围为
,由抛物线的图象即可得△BDP的取值范围为![]() ,因
,因![]() 即可得平行四边形BDQP面积的取值范围为
即可得平行四边形BDQP面积的取值范围为![]() ;(2)过点P作PG⊥AB,设A(
;(2)过点P作PG⊥AB,设A(![]() ,0),B(
,0),B(![]() ,0),P(
,0),P(![]() ,
, ![]() ),由PG∥
),由PG∥![]() 轴,根据相似三角形的判定方法可得
轴,根据相似三角形的判定方法可得![]() ,
, ![]() ,再由相似三角形的性质可得
,再由相似三角形的性质可得![]() ,
, ![]() ,代入数值可得
,代入数值可得![]() ,
, ![]() ,把这两个式子相加可得
,把这两个式子相加可得![]() ,令
,令![]() ,即可得
,即可得![]() ,
, ![]() ,所以
,所以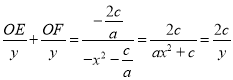 ,即
,即![]() ,所以
,所以![]() ,即可得
,即可得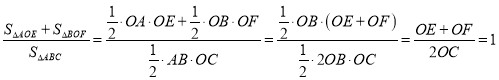
所以可得结论![]() 与
与![]() 、
、![]() 无关,比值为1.
无关,比值为1.
试题解析:
(1)①![]()
②连接DB、OP,设P(![]() ,
, ![]() )
)
∵A(-2,0),对称轴为![]() 轴
轴
∴B(2,0)
∴![]()
![]()
![]()
![]()
∵点P在第四象限运动
∴![]()
∴由抛物线的图象可得: ![]()
∵![]() ∴
∴![]()
(2)过点P作PG⊥AB,设A(![]() ,0),B(
,0),B(![]() ,0),P(
,0),P(![]() ,
, ![]() )
)

∴PG∥![]() 轴
轴
∴![]() ,
, ![]()
∴![]() ,
, ![]()
∴![]() ,
, ![]()
∴![]()
∵当![]() 时,∴
时,∴![]() ,即
,即![]() ,
, ![]()
∴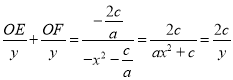
∴![]() ∴
∴![]()
∴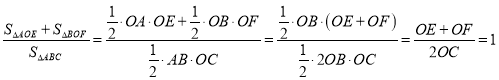
∴![]() 与
与![]() 、
、![]() 无关,比值为1.
无关,比值为1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】算式(﹣20)﹣(+3)﹣(+5)﹣(﹣7)写成省略加号的和的形式正确的为( )
A.20+3+5﹣7
B.﹣20﹣3﹣5﹣7
C.﹣20﹣3+5+7
D.﹣20﹣3﹣5+7 -
科目: 来源: 题型:
查看答案和解析>>【题目】随着交通网络的不断完善.旅游业持续升温,据统计,在今年“五一”期间,某风景区接待游客403000人,这个数据用科学记数法表示为( )
A.403×103
B.40.3×104
C.4.03×105
D.0.403×106 -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两位同学参加数学素质测试,各项成绩如下(单位:分)

(1)分别计算甲、乙成绩的中位数;
(2)如果数与代数、空间与图形、统计与概率、综合与实践的成绩按3:3:2:2计算,那么甲、乙的数学素质测试平均成绩分别为多少分?
-
科目: 来源: 题型:
查看答案和解析>>【题目】“两条直线相交只有一个交点”的题设是( )
A. 两条直线 B. 相交
C. 只有一个交点 D. 两条直线相交
-
科目: 来源: 题型:
查看答案和解析>>【题目】国家规定,中小学生每天在校体育活动时间不低于1小时,为了解这项政策的落实情况,有关部门就“你某天在校体育活动时间是多少”的问题,在某校随机抽查了部分学生,再根据活动时间t(小时)进行分组(A组:t<0.5,B组:0.5≤t<1,C组:1≤t<1.5,D组:t≥1.5),绘制成如下两幅不完整统计图,请根据图中信息回答问题:

(1)此次抽查的学生数为 人,并补全条形统计图;
(2)从抽查的学生中随机询问一名学生,该生当天在校体育活动时间低于1小时的概率是 ;
(3)若当天在校学生数为1200人,请估计在当天达到国家规定体育活动时间的学生有 人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程3x2﹣6x+m=0有两个不相等的实数根,则m的取值范围是( )
A.m<3
B.m≤3
C.m>3
D.m≥3
相关试题

