【题目】在平面直角坐标系中,点A(a ,2![]() )是直线y=
)是直线y=![]() x上一点,以A为圆心,2为半径作⊙A,若P(x,y)是第一象限内⊙A上任意一点,则
x上一点,以A为圆心,2为半径作⊙A,若P(x,y)是第一象限内⊙A上任意一点,则![]() 的最小值为( )
的最小值为( )
A. 1 B. ![]() C.
C. ![]() —1 D.
—1 D. ![]()
参考答案:
【答案】D
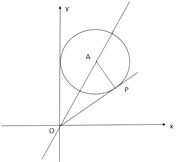
【解析】分析: 如图所示,当直线OP与圆A相切时,连接AP,过P作PH⊥x轴,此时![]() 取得最小值,利用切线的性质得到AP垂直于OP,在直角三角形AOP中,根据到角两边距离相等的点在角的平分线上确定出∠AOP=30°,
取得最小值,利用切线的性质得到AP垂直于OP,在直角三角形AOP中,根据到角两边距离相等的点在角的平分线上确定出∠AOP=30°,![]() 为tan∠30°的值,求出即可.
为tan∠30°的值,求出即可.
详解: 如图所示,当直线OP与圆A相切时,连接AP,过P作PH⊥x轴,此时![]() 取得最大值,
取得最大值,
∵点A(a ,2![]() )是直线y=
)是直线y=![]() x上一点,
x上一点,
∴a=2,
∴A(2 ,2![]() ).
).
∵以A为圆心,2为半径作⊙A,
∴⊙A与y轴相切.
则当直线OP与圆A相切时, ![]() 取得最小值,
取得最小值,
∵∠AOy=∠AOP=30°,
∴∠AOx=30°,
∴此时![]() =tan30°=
=tan30°=![]() ,
,
则![]() 的最小值为
的最小值为![]() .
.
故选:D.
点睛:
此题考查了切线的性质,坐标与图形性质,以及锐角三角函数定义,熟练掌握切线的性质是解本题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l上有一点O,点A,B同时从O出发,在直线l上分别向左,向右作匀速运动,且A,B的速度之比是1:2,设运动时间为ts,
(1)当t=2s时,AB=24cm,此时,
①在直线l上画出A,B两点运动2s时的位置,并回答点A运动的速度是 cm/s,点B的运动速度是 cm/s;
②若点P为直线l上一点,且PA=OP+PB,求
 的值;
的值;(2)在(1)的条件下,若A,B同时按原速度向左运动,再经过几秒,OA=3OB?

-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填入相应集合的括号内.
+8.5,﹣3
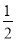 ,0.3,0,﹣3.4,12,﹣9,﹣1.2,20%,﹣2.
,0.3,0,﹣3.4,12,﹣9,﹣1.2,20%,﹣2.(1)正数集合:{_____…};
(2)整数集合:{_____…};
(3)非正整数集合:{_____…};
(4)负分数集合:{_____…}.
-
科目: 来源: 题型:
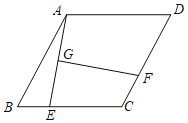
查看答案和解析>>【题目】如图,四边形ABCD为菱形,∠D=60°,AB=4,E为边BC上的动点,连接AE,作AE的垂直平分线GF交直线CD于F点,垂足为点G,则线段GF的最小值为____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某农科所对甲、乙两种小麦各选用10块面积相同的试验田进行种植试验,它们的平均亩产量分别是
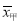 =610千克,
=610千克, 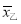 =609千克,亩产量的方差分别是
=609千克,亩产量的方差分别是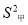 =29.6,
=29.6, 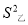 =2.则关于两种小麦推广种植的合理决策是( )
=2.则关于两种小麦推广种植的合理决策是( )A. 甲的平均亩产量较高,应推广甲
B. 甲、乙的平均亩产量相差不多,均可推广
C. 甲的平均亩产量较高,且亩产量比较稳定,应推广甲
D. 甲、乙的平均亩产量相差不多,但乙的亩产量比较稳定,应推广乙
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系xOy中,直线y=
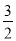 x+b与直线y=
x+b与直线y=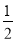 x交于点A(m,1).与y轴交于点B
x交于点A(m,1).与y轴交于点B(1)求m的值和点B的坐标;
(2)若点C在y轴上,且△ABC的面积是1,请直接写出点C的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为绿化校园,安排七年级三个班植树,其中,一班植树x棵,二班植树的棵数是一班的2倍少20棵,三班植树的棵数是二班的一半多15棵.
(1)三个班共植树多少棵?(用含x的式子表示)
(2)当x=30时,三个班中哪个班植树最多?
相关试题

