【题目】某校准备组织290名学生进行野外考察活动,行李件数比学生人数的一半还少45.学校计划租用甲、乙两种型号的汽车共8辆,经了解,甲种汽车每辆最多能载40人和10件行李,乙种汽车最多能载30人和20件行李.
(1)求行李有多少件?
(2)现计划租用甲种汽车x辆,请你帮学校设计所有可能的租车方案.
(3)如果甲、乙两种汽车每辆的租车费分别是2000元、1800元,请你选择最省钱的一种租车方案,并求出至少的费用是多少元.
参考答案:
【答案】(1)100;(2) 共有2种租车方案:方案一:租用甲种汽车5辆,乙种汽车3辆;方案二:租用甲种汽车6辆,乙种汽车2辆;(3) 租用甲种汽车5辆,乙种汽车3辆的方案更省费用
【解析】
(1)首先依据行李件数比学生人数的一半还少45求得行李的件数;
(2)然后依据8辆车能乘载的人数大于等于290人,能够装载的行李的件数大于等于100列不等式组求解即可;
(3)本题可分别计算甲、乙所需要的费用,然后比较,花费较少的即为最省钱的租车方案
(1)∵行李件数比学生人数的一半还少45,
∴行李的件数![]()
(2)由租用甲种汽车x辆,则租用乙种汽车(8x)辆,
由题意得:![]()
解得:![]()
所以共有2种租车方案:方案一:租用甲种汽车5辆,乙种汽车3辆;方案二:租用甲种汽车6辆,乙种汽车2辆。
(3)第一种租车方案的费用为5×2000+3×1800=15400(元);
第二种租车方案的费用为6×2000+2×1800=15600(元).
∴租用甲种汽车5辆,乙种汽车3辆的方案更省费用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】是否存在整数m,使关于x的不等式1+
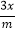 >
> +
+ 与关于x的不等式x+1>
与关于x的不等式x+1> 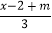 的解集相同?若存在,求出整数m和不等式的解集;若不存在,请说明理由.
的解集相同?若存在,求出整数m和不等式的解集;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某福利工厂准备在六一前夕准备生产甲、乙两种型号的玩具送给一所幼儿园,已知生产甲型玩具需要1号配件7个,2号配件2个;生产乙型玩具需要1号配件3个,2号配件5个,生产现有1号配件480个,2号配件370个,若该厂计划生产甲乙两种型号的玩具一共100个,用现有配件能否完成计划?如能,请写出所有的生产方案;如不能则说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ABC=90°,O为射线BC上一点,以点O为圆心,
 OB长为半径作⊙O,将射线BA绕点B按顺时针方向旋转至BA′,若BA′与⊙O相切,则旋转的角度α(0°<α<180°)等于 .
OB长为半径作⊙O,将射线BA绕点B按顺时针方向旋转至BA′,若BA′与⊙O相切,则旋转的角度α(0°<α<180°)等于 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据下列要求,解答相关问题.
请补全以下求不等式﹣2x2﹣4x>0的解集的过程.
①构造函数,画出图象:根据不等式特征构造二次函数y=﹣2x2﹣4x;并在下面的坐标系中(图1)画出二次函数y=﹣2x2﹣4x的图象(只画出图象即可).
②求得界点,标示所需,当y=0时,求得方程﹣2x2﹣4x=0的解为;并用锯齿线标示出函数y=﹣2x2﹣4x图象中y>0的部分.
③借助图象,写出解集:由所标示图象,可得不等式﹣2x2﹣4x>0的解集为﹣2<x<0.请你利用上面求一元一次不等式解集的过程,求不等式x2﹣2x+1≥4的解集.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某县政府为了迎接“八一”建军节,加强军民共建活动,计划从花园里拿出1430盆甲种花卉和1220盆乙种花卉,搭配成A、B两种园艺造型共20个,在城区内摆放,以增加节日气氛,已知搭配A、B两种园艺造型各需甲、乙两种花卉数如表所示:(单位:盆)
(1)某校某年级一班课外活动小组承接了这个园艺造型搭配方案的设计,问符合题意的搭配方案有几种?请你帮忙设计出来.
(2)如果搭配及摆放一个A造型需要的人力是8人次,搭配及摆放一个B造型需要的人力是11人次,哪种方案使用人力的总人次数最少,请说明理由.
造型数量花
A
B
甲种
80
50
乙种
40
90
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,CD是AB边上的高,AC=4,BC=3,DB=


求:(1)求AD的长;
(2)△ABC是直角三角形吗?为什么?
相关试题

