【题目】如图,已知反比例函数y=![]() 与一次函数y=k2x+b的图象交于点A(1,8)、B(﹣4,m).
与一次函数y=k2x+b的图象交于点A(1,8)、B(﹣4,m).
(1)求k1、k2、b的值;
(2)求△AOB的面积;
(3)若M(x1 , y1)、N(x2 , y2)是反比例函数y=![]() 图象上的两点,且x1<x2 , y1<y2 , 指出点M、N各位于哪个象限,并简要说明理由.
图象上的两点,且x1<x2 , y1<y2 , 指出点M、N各位于哪个象限,并简要说明理由.
参考答案:
【答案】
(1)
解:∵反比例函数y=![]() 与一次函数y=k2x+b的图象交于点A(1,8)、B(﹣4,m),
与一次函数y=k2x+b的图象交于点A(1,8)、B(﹣4,m),
∴k1=8,B(﹣4,﹣2),
解![]() ,解得
,解得![]() ;
;
(2)
解:由(1)知一次函数y=k2x+b的图象与y轴的交点坐标为C(0,6),
∴S△AOB=S△COB+S△AOC=![]() ×6×4+
×6×4+![]() ×6×1=15;
×6×1=15;
(3)
解∵比例函数y=![]() 的图象位于一、三象限,
的图象位于一、三象限,
∴在每个象限内,y随x的增大而减小,
∵x1<x2,y1<y2,
∴M,N在不同的象限,
∴M(x1,y1)在第三象限,N(x2,y2)在第一象限.
【解析】(1)先把A点坐标代入y=![]() 可求得k1=8,则可得到反比例函数解析式,再把B(﹣4,m)代入反比例函数求得m,得到B点坐标,然后利用待定系数法确定一次函数解析式即可求得结果;
可求得k1=8,则可得到反比例函数解析式,再把B(﹣4,m)代入反比例函数求得m,得到B点坐标,然后利用待定系数法确定一次函数解析式即可求得结果;
(2)由1知一次函数y=k2x+b的图象与y轴的交点坐标为(0,6),可求S△AOB=![]() ×6×2+
×6×2+![]() ×6×1=15;
×6×1=15;
(3)根据反比例函数的性质即可得到结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在四边形ABCD中,点E、F分别是AB、CD的中点,过点E作AB的垂线,过点F作CD的垂线,两垂线交于点G,连接AG、BG、CG、DG,且∠AGD=∠BGC.
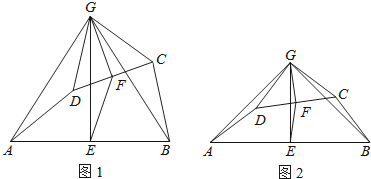
(1)求证:AD=BC;
(2)求证:△AGD∽△EGF;
(3)如图2 , 若AD、BC所在直线互相垂直,求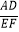 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某旅游景点的门票价格如下表:
购票人数(单位人)
1﹣50
51﹣100
100以上
每人门票价(单位元)
80
75
70
某旅行社计划帶甲、乙两个旅行团共100多人计划去游览该景点,其中甲旅行团人数少于50人,乙旅行团人数有50 多人但不足100人,如果两旅行团都以各自团体为单位单独购票,则一共支付7965元;如果两旅行团联合起来作为一个团体购票,则只管花费7210元.间两旅行团各有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司需招聘一名员工,对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核.甲、乙、丙各项得分如下表:
笔 试
面 试
体 能
甲
85
80
75
乙
80
90
73
丙
83
79
90
(1)根据三项得分的平均分,从高到低确定三名应聘者的排名顺序.
(2)该公司规定:笔试,面试、体能得分分别不得低于80分,80分,70分,并按60%,30%,10%的比例计入总分(不计其他因素条件),请你说明谁将被录用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.

(1)填空:∠ABC= , BC=;
(2)判断△ABC与△DEF是否相似?并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】在⊙O中,直径AB=6,BC是弦,∠ABC=30°,点P在BC上,点Q在⊙O上,且OP⊥PQ.
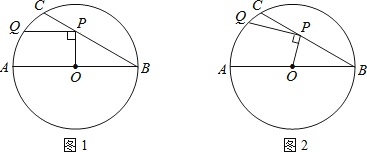
(1)如图1,当PQ∥AB时,求PQ的长度;
(2)如图2,当点P在BC上移动时,求PQ长的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=36°,∠C=72°,∠ABC的平分线交AC于D,则图中共有等腰三角形( )

A.0个 B.1个 C.2个 D.3个
相关试题

