搜索
【题目】二次函数y=ax2+bx+c（a≠0）和正比例函数y= 
x的图象如图所示，则方程ax2+（b﹣ ）x+c=0（a≠0）的两根之和（ ） 
A.大于0
B.等于0
C.小于0
D.不能确定
参考答案：
【答案】A
【解析】解：设ax2+bx+c=0（a≠0）的两根为x1 ， x2 ， ∵由二次函数的图象可知x1+x2＞0，a＞0，
∴﹣ 
＞0．
设方程ax2+（b﹣ 
）x+c=0（a≠0）的两根为m，n，则m+n=﹣ 
=﹣ + 
，
∵a＞0，
∴ ＞0，
∴m+n＞0．
故选A．
设ax2+bx+c=0（a≠0）的两根为x1 ， x2 ， 由二次函数的图象可知x1+x2＞0，a＞0，设方程ax2+（b﹣ ）x+c=0（a≠0）的两根为m，n再根据根与系数的关系即可得出结论．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在大楼AB的正前方有一斜坡CD，已知斜坡CD长6
米，坡角∠DCE等于45°，小红在斜坡下的点C处测得楼顶B的仰角为60°，在斜坡上的顶点D处测得楼顶B的仰角为45°，其中点A、C、E在同一直线上．
（1）求斜坡CD的高度DE；
（2）求大楼AB的高度（结果保留根号）． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，以矩形ABCD的对角线AC的中点O为圆心，OA长为半径作⊙O，过点B作BK⊥AC，垂足为K，过D作DH∥KB，DH分别与AC，AB，⊙O及CB的延长线相交于点E，F，G，H，且F是EG的中点．
（1）求证：点D在⊙O上；
（2）求证：F是AB的中点；
（3）若DE=4，求⊙O的半径和△BFH的面积． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y=ax2+bx﹣2经过点A（1，0）和点B（4，0），与y轴交于点C．
附：阅读材料
法国弗朗索瓦韦达最早发现一元二次方程中根与系数的关系为：两根之和等于一次项系数与二次项系数之比的相反数，两根之积等于常数项羽二次项系数之比，人们称之为韦达定理．
即：设一元二次方程ax2+bx+c=0的两根为x1、x2 ， 则：x1+x2=﹣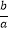
，x1x2= 
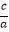能灵活运用韦达定理，有时可以使解题更为简单．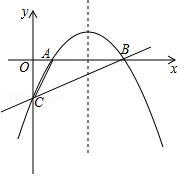
（1）求抛物线的解析式；
（2）以点A为圆心，作于直线BC相切的⊙A，求⊙A的面积；
（3）将直线BC向下平移n个单位后与抛物线交于点M、N，且线段MN=2CB，求直线MN的解析式及平移距离． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在矩形ABCD中，E是AD边的中点，BE⊥AC，垂足为点F，连接DF，分析下列四个结论：①△AEF∽△CAB；②CF=2AF；③DF=DC；④tan∠CAD=
；正确的是（ ） 
A.4个
B.3个
C.2个
D.1个 -
科目： 来源： 题型：
查看答案和解析>>【题目】抛物线y=﹣
x+2与y轴交于点A，顶点为B．点P是x轴上的一个动点，当点P的坐标是时，|PA﹣PB|取得最小值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图放置的△OAB1 ， △B1A1B2 ， △B2A2B3 ， …都是边长为2的等边三角形，边AO在y轴上，点B1 ， B2 ， B3 ， …都在直线y=
x上，则A2014的坐标是 ． 
相关试题
