【题目】如图,△ABC是⊙O的内接三角形,AB是⊙O的直径,OD⊥AB于点O,分别交AC、CF于点E、D,且DE=DC.

(1)求证:CF是⊙O的切线;
(2)若⊙O的半径为5,BC=![]() ,求DE的长.
,求DE的长.
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)连接OC,欲证明CF是⊙O的切线,只要证明∠OCF=90°.
(2)作DH⊥AC于H,由△AEO∽△ABC,得![]() 求出AE,EC,再根据sin∠A=sin∠EDH,得到
求出AE,EC,再根据sin∠A=sin∠EDH,得到![]() ,求出DE即可.
,求出DE即可.
试题解析:连接OC,∵OA=OC,∴∠A=∠OCA,∵OD⊥AB,∴∠A+∠AEO=90°,∵DE=DC,∴∠DEC=∠DCE,∵∠AEO=∠DCE,∴∠AEO=∠DCE,∴∠OCE+∠DCE=90°,∠OCF=90°,∴OC⊥CF,∴CF是⊙O切线.
(2)作DH⊥AC于H,则∠EDH=∠A,∵DE=DC,∴EH=HC=![]() EC,∵⊙O的半径为5,BC=
EC,∵⊙O的半径为5,BC=![]() ,∴AB=10,AC=
,∴AB=10,AC=![]() ,∵△AEO∽△ABC,∴
,∵△AEO∽△ABC,∴![]() ,∴AE=
,∴AE=![]() ,∴EC=AC﹣AE=
,∴EC=AC﹣AE=![]() ,∴EH=
,∴EH=![]() EC=
EC=![]() ,∵∠EDH=∠A,∴sin∠A=sin∠EDH,∴
,∵∠EDH=∠A,∴sin∠A=sin∠EDH,∴![]() ,∴DE=
,∴DE=![]() =
= =
=![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
在数学课上,老师请同学思考如下问题:如图1,我们把一个四边形ABCD的四边中点E,F,G,H依次连接起来得到的四边形EFGH是平行四边形吗?
小敏在思考问题时,有如下思路:连接AC.

结合小敏的思路作答:
(1)若只改变图1中四边形ABCD的形状(如图2),则四边形EFGH还是平行四边形吗?说明理由,参考小敏思考问题的方法解决一下问题;
(2)如图2,在(1)的条件下,若连接AC,BD.
①当AC与BD满足什么条件时,四边形EFGH是菱形,写出结论并证明;
②当AC与BD满足什么条件时,四边形EFGH是矩形,直接写出结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料,然后解答后面的问题。
我们知道方程
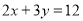 有无数组解,但在实际生活中我们往往只需要求出其正整数解。例:由
有无数组解,但在实际生活中我们往往只需要求出其正整数解。例:由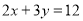 ,得
,得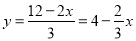 ,(
,( 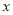 、
、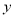 为正整数)
为正整数) 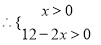 则有
则有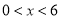 .又
.又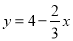 为正整数,则
为正整数,则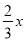 为整数.
为整数.由2与3互质,可知:
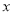 为3的倍数,从而
为3的倍数,从而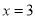 ,代入
,代入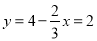 .
.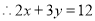 的正整数解为
的正整数解为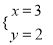
问题:(1)若
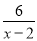 为自然数,则满足条件的
为自然数,则满足条件的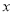 值有_____________个
值有_____________个(2)请你写出方程
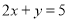 的所有正整数解:_________________________
的所有正整数解:_________________________(3)若
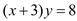 ,请用含
,请用含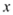 的式子表示
的式子表示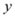 ,并求出它的所有整数解。
,并求出它的所有整数解。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一垂直于地面的灯柱AB被一钢筋CD固定,CD与地面成45°夹角(∠CDB=45°),在C点上方2米处加固另一条钢线ED,ED与地面成53°夹角(∠EDB=53°),那么钢线ED的长度约为多少米?(结果精确到1米,参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)
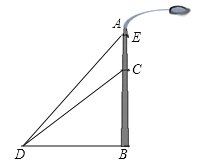
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知抛物线y=x2+bx+c过A,B,C三点,点A的坐标是(3,0),点C的坐标是(0,-3),动点P在抛物线上.
(1)b =_________,c =_________,点B的坐标为_____________;(直接填写结果)
(2)是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;
(3)过动点P作PE垂直y轴于点E,交直线AC于点D,过点D作x轴的垂线.垂足为F,连接EF,当线段EF的长度最短时,求出点P的坐标.
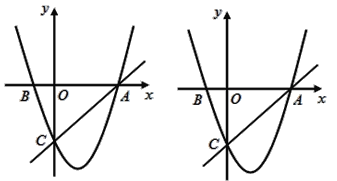
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两双曲线y=
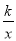 与y=﹣
与y=﹣ 分别位于第一、四象限,A是y轴上任意一点,B是y=﹣
分别位于第一、四象限,A是y轴上任意一点,B是y=﹣ 上的点,C是y=
上的点,C是y=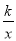 上的点,线段BC⊥x轴于点 D,且4BD=3CD,则下列说法:①双曲线y=
上的点,线段BC⊥x轴于点 D,且4BD=3CD,则下列说法:①双曲线y=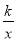 在每个象限内,y随x的增大而减小;②若点B的横坐标为3,则点C的坐标为(3,﹣
在每个象限内,y随x的增大而减小;②若点B的横坐标为3,则点C的坐标为(3,﹣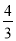 );③k=4;④△ABC的面积为定值7,正确的有( )
);③k=4;④△ABC的面积为定值7,正确的有( )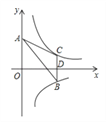
A. B. C. D. ④
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商品进货单价为30元,按40元一个销售能卖40个;若销售单价每涨1元,则销量减少1个.为了获得最大利润,此商品的最佳售价应为__元.
相关试题

