【题目】已知抛物线![]() ,其中
,其中![]() ,且
,且![]() .
.
(1)直接写出关于![]() 的一元二次方程
的一元二次方程![]() 的一个根;
的一个根;
(2)证明:抛物线![]() 的顶点
的顶点![]() 在第三象限;
在第三象限;
(3)直线![]() 与
与![]() 轴分别相交于
轴分别相交于![]() 两点,与抛物线
两点,与抛物线![]() 相交于
相交于![]() 两点.设抛物线
两点.设抛物线![]() 的对称轴与
的对称轴与![]() 轴相交于
轴相交于![]() ,如果在对称轴左侧的抛物线上存在点
,如果在对称轴左侧的抛物线上存在点![]() ,使得
,使得![]() 与
与![]() 相似.并且
相似.并且![]() ,求此时抛物线的表达式.
,求此时抛物线的表达式.

参考答案:
【答案】(1)x=1(2)证明见解析(3)y=x2+2x﹣3
【解析】
试题分析:(1)根据a+b+c=0,结合方程确定出方程的一个根即可;
(2)表示出抛物线的对称轴,将2a=b代入,并结合a+b+c=0,表示出c,判断顶点坐标即可;
(3)根据表示出的b与c,求出方程的解确定出抛物线解析式,由直线y=x+m与x,y轴交于B,C两点,表示出OB=OC=|m|,可得出三角形BOC为等腰直角三角形,确定出三角形三角形ADE面积,根据三角形ADF等于三角形ADE面积的一半求出a的值,即可确定出抛物线解析式.
试题解析:(1)∵抛物线y=ax2+bx+c,a+b+c=0,
∴关于x的一元二次方程ax2+bx+c=0的一个根为x=1;
(2)证明:∵2a=b,
∴对称轴x=﹣![]() =﹣1,
=﹣1,
把b=2a代入a+b+c=0中得:c=﹣3a,
∵a>0,c<0,
∴△=b2﹣4ac>0,
∴![]() <0,
<0,
则顶点A(﹣1,![]() )在第三象限;
)在第三象限;
(3)由b=2a,c=﹣3a,得到x=![]() =
=![]() ,
,
解得:x1=﹣3,x2=1,
二次函数解析式为y=ax2+2ax﹣3a,
∵直线y=x+m与x,y轴分别相交于点B,C两点,则OB=OC=|m|,
∴△BOC是以∠BOC为直角的等腰直角三角形,即此时直线y=x+m与对称轴x=﹣1的夹角∠BAE=45°,
∵点F在对称轴左侧的抛物线上,则∠DAF>45°,此时△ADF与△BOC相似,
顶点A只可能对应△BOC的直角顶点O,即△ADF是以A为直角顶点的等腰直角三角形,且对称轴为x=﹣1,
设对称轴x=﹣1与OF交于点G,
∵直线y=x+m过顶点A(﹣1,﹣4a),
∴m=1﹣4a,
∴直线解析式为y=x+1﹣4a,
联立得: ,
,
解得:![]() 或
或 ,
,
这里(﹣1,﹣4a)为顶点A,(![]() ﹣1,
﹣1,![]() ﹣4a)为点D坐标,
﹣4a)为点D坐标,
点D到对称轴x=﹣1的距离为![]() ﹣1﹣(﹣1)=
﹣1﹣(﹣1)=![]() ,AE=|﹣4a|=4a,
,AE=|﹣4a|=4a,
∴S△ADE=![]() ×
×![]() ×4a=2,即它的面积为定值,
×4a=2,即它的面积为定值,
这时等腰直角△ADF的面积为1,
∴底边DF=2,
而x=﹣1是它的对称轴,此时D、C重合且在y轴上,由![]() ﹣1=0,
﹣1=0,
解得:a=1,此时抛物线解析式为y=x2+2x﹣3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 市首批一次性投放公共自行车700辆供市民租用出行,由于投入数量不够, 导致出现需要租用却未租到车的现象,现随机抽取的某五天在同一时段的调查数据汇成如下表格.
市首批一次性投放公共自行车700辆供市民租用出行,由于投入数量不够, 导致出现需要租用却未租到车的现象,现随机抽取的某五天在同一时段的调查数据汇成如下表格.请回答下列问题:
时间
第一天7:00﹣8:00
第二天7:00﹣8:00
第三天7:00﹣8:00
第四天7:00﹣8:00
第五天7:00﹣8:00
需要租用自行车却未租到车的人数(人)
1500
1200
1300
1300
1200
(1)表格中的五个数据(人数)的中位数是多少?
(2)由随机抽样估计,平均每天在7:00-8:00 :需要租用公共自行车的人数是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)(π﹣2013)0﹣( )﹣2+|﹣4|
)﹣2+|﹣4|
(2)4(a+2)(a+1)﹣7(a+3)(a﹣3) -
科目: 来源: 题型:
查看答案和解析>>【题目】化简:
(1)﹣(a2﹣b)2+(2a+b)(﹣2a+b);
(2)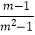 ÷(m﹣1﹣
÷(m﹣1﹣ 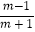 ).
). -
科目: 来源: 题型:
查看答案和解析>>【题目】计算(﹣x2y3)3(﹣xy2)的结果是( )
A.﹣x7y11
B.x7y11
C.x6y8
D.﹣x7y8 -
科目: 来源: 题型:
查看答案和解析>>【题目】若x2- mx + 16是完全平方式,则m的值是( )
A.8B.- 8C.8 或 – 8D.16 或 - 16
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,四边形
 中,
中,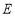 是对角线
是对角线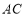 上一点,
上一点,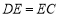 ,以
,以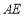 为直径的
为直径的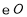 与边
与边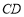 相切于点
相切于点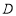 .
.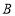 点在
点在 上,连接
上,连接 .
.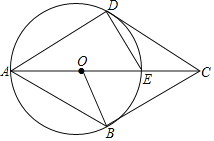
(1)求证:
 ;
;(2)若
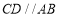 ,求证:四边形
,求证:四边形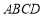 是菱形.
是菱形.
相关试题

