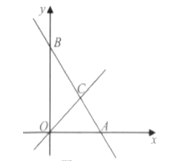
【题目】如下图,在平面直角坐标系中,直线AB与x轴交于点A,与y轴交于点B,与直线OC:y=x交于点C.
(1)若直线AB解析式为![]() .
.
①求点C的坐标;
②根据图象,求关于x的不等式0<-![]() x+10<x的解集;
x+10<x的解集;
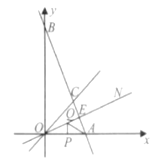
(2)如下图,作∠AOC的平分线ON,若AB⊥ON,垂足为E,ΔOAC的面积为9,且OA=6,P、Q分别为线段OA、OE上的动点,连接AQ与PQ,试探索AQ+PQ是否存在最小值?若存在,求出这个最小值:若不存在,说明理由.
参考答案:
【答案】(1)①C(4,4) ,②4<x<![]() ;(2) AQ+PQ存在最小值,最小值为3.
;(2) AQ+PQ存在最小值,最小值为3.
【解析】
(1)①根据直线AB和直线OC相交于点C,将两个函数解析式联立,解方程组即为C(4,4);②先求出A点坐标,观察图像即可得出不等式的解集为4<x<![]() ;
;
(2)首先在OC上截取OM=OP,连接MQ,通过SAS定理判定△POQ≌△MOQ,从而得出PQ=MQ,进行等式变换AQ+PQ=AQ+MQ,,即可判断当A、Q、M在同一直线上,且AM⊥0C时,AQ+MQ最小,即AQ+PQ存在最小值;再由ASA定理判定△AEO≌ΔCEO,最后由OC=OA=6,ΔOAC的面积为9,得出AM=3.
(1)①由題意,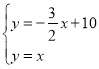
解得:![]()
所以C(4,4)
②把y=0代入![]() ,
,
解得![]()
所以A点坐标为(![]() ,0),
,0),
∵C(4,4),
所以观察图像可得:不等式的解集为4<x<![]() ;
;
(2)由题意,在OC上截取OM=OP,连接MQ,
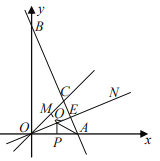
∵ON平分∠AOC,
∴∠AOQ=∠COQ,
又OQ=OQ.
∴△POQ≌△MOQ(SAS),
∴PQ=MQ,
∴AQ+PQ=AQ+MQ,
当A、Q、M在同一直线上,且AM⊥OC时,AQ+MQ最小,
即AQ+PQ存在最小值
∴AB⊥ON,所以∠AEO=∠CEO,
∴△AEO≌ΔCEO(ASA),
∴OC=OA=6,
∵ΔOAC的面积为9,
∴![]() OC·AM=9,
OC·AM=9,
∴AM=3,
:AQ+PQ存在最小值,最小值为3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方形ABC1D1的边长为1,延长C1D1到A1,以A1C1为边向右作正方形A1C1C2D2,延长C2D2到A2,以A2C2为边向右作正方形A2C2C3D3(如图所示),以此类推…,若A1C1=2,且点A,D2, D3,…,D10都在同一直线上,则正方形A9C9C10D10的边长是______
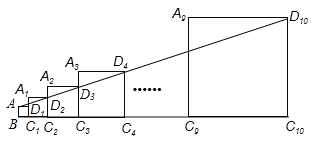
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-1,4),C(-3,2).
(1)以原点O为位似中心,相似比为1∶2,在y轴的左侧,画出△ABC放大后的图形△A1B1C1,并直接写出C1点的坐标;
(2)若点D(a,b)在线段AB上,请直接写出经过(1)的变化后点D的对应点D1的坐标.
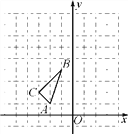
-
科目: 来源: 题型:
查看答案和解析>>【题目】一天,王亮同学从家里跑步到体育馆,在那里锻炼了一阵后又走到某书店去买书,然后散步走回家如图反映的是在这一过程中,王亮同学离家的距离s(千米)与离家的时间t(分钟)之间的关系,请根据图象解答下列问题:
(1)体育馆离家的距离为多少千米,书店离家的距离为多少千米;王亮同学在书店待了多少分钟.
(2)分别求王亮同学从体育馆走到书店的平均速度和从书店出来散步回家的平均速度.
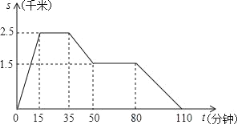
-
科目: 来源: 题型:
查看答案和解析>>【题目】Rt△ABC 中,∠BAC=90°,AB=AC=2,以 AC 为一边.在△ABC 外部作等腰直角三角形ACD ,则线段 BD 的长为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市茶叶专卖店销售某品牌茶叶,其进价为每千克 240 元,按每千克 400 元出售,平均每周可售出 200 千克,后来经过市场调查发现,单价每降低 10 元,则平均每周的销售量可增加 40 千克,若该专卖店销售这种品牌茶叶要想平均每周获利 41600 元,请回答:
(1)每千克茶叶应降价多少元?
(2)在平均每周获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的 几折出售?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,CD是边AB上的高,且
 .
.(1)求证:△ACD∽△CBD;
(2)求∠ACB的大小.

相关试题

