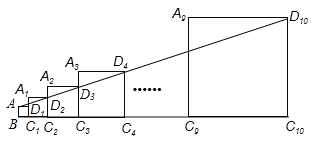
【题目】已知正方形ABC1D1的边长为1,延长C1D1到A1,以A1C1为边向右作正方形A1C1C2D2,延长C2D2到A2,以A2C2为边向右作正方形A2C2C3D3(如图所示),以此类推…,若A1C1=2,且点A,D2, D3,…,D10都在同一直线上,则正方形A9C9C10D10的边长是______
参考答案:
【答案】![]() .
.
【解析】试题解析:延长D4A和C1B交于O,
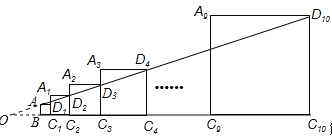
∵AB∥A2C1,
∴△AOB∽△D2OC2,
∴![]() ,
,
∵AB=BC1=1,D 2C2=C1C2=2,
∴![]()
∴OC2=2OB,
∴OB=BC2=3,
∴OC2=6,
设正方形A2C2C3D3的边长为x1,
同理证得:△D2OC2∽△D3OC3,
∴![]() ,解得,x1=3,
,解得,x1=3,
∴正方形A2C2C3D3的边长为3,
设正方形A3C3C4D4的边长为x2,
同理证得:△D3OC3∽△D4OC4,
∴![]() ,解得x2=
,解得x2=![]() ,
,
∴正方形A3C3C4D4的边长为![]() ;
;
设正方形A4C4C5D5的边长为x3,
同理证得:△D4OC4∽△D5OC5,
∴ ,解得x=
,解得x=![]() ,
,
∴正方形A4C4C5D5的边长为![]() ;
;
以此类推….
正方形An-1Cn-1CnDn的边长为![]() ;
;
∴正方形A9C9C10D10的边长为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将长方形ABCD沿着对角线BD折叠,使点C落在C′处,BC′交AD于点E.
(1)若∠DBC=25°,求∠ADC′的度数;
(2)若AB=4,AD=8,求△BDE的面积.

-
科目: 来源: 题型:
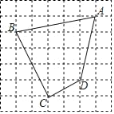
查看答案和解析>>【题目】如图,每个小正方形的边长都为1,四边形ABCD的顶点都在小正方形的顶点上.
(1)求四边形ABCD的面积;
(2)∠BCD是直角吗?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于点G,BG=4
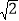 ,则△EFC的周长为( )
,则△EFC的周长为( )
A. 11 B. 10 C. 9 D. 8
-
科目: 来源: 题型:
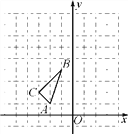
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-1,4),C(-3,2).
(1)以原点O为位似中心,相似比为1∶2,在y轴的左侧,画出△ABC放大后的图形△A1B1C1,并直接写出C1点的坐标;
(2)若点D(a,b)在线段AB上,请直接写出经过(1)的变化后点D的对应点D1的坐标.
-
科目: 来源: 题型:
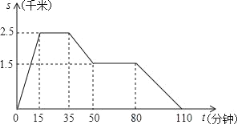
查看答案和解析>>【题目】一天,王亮同学从家里跑步到体育馆,在那里锻炼了一阵后又走到某书店去买书,然后散步走回家如图反映的是在这一过程中,王亮同学离家的距离s(千米)与离家的时间t(分钟)之间的关系,请根据图象解答下列问题:
(1)体育馆离家的距离为多少千米,书店离家的距离为多少千米;王亮同学在书店待了多少分钟.
(2)分别求王亮同学从体育馆走到书店的平均速度和从书店出来散步回家的平均速度.
-
科目: 来源: 题型:
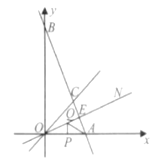
查看答案和解析>>【题目】如下图,在平面直角坐标系中,直线AB与x轴交于点A,与y轴交于点B,与直线OC:y=x交于点C.
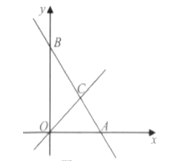
(1)若直线AB解析式为
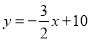 .
.①求点C的坐标;
②根据图象,求关于x的不等式0<-
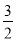 x+10<x的解集;
x+10<x的解集;(2)如下图,作∠AOC的平分线ON,若AB⊥ON,垂足为E,ΔOAC的面积为9,且OA=6,P、Q分别为线段OA、OE上的动点,连接AQ与PQ,试探索AQ+PQ是否存在最小值?若存在,求出这个最小值:若不存在,说明理由.
相关试题

