【题目】如图,△ABC中,CD是边AB上的高,且![]() .
.
(1)求证:△ACD∽△CBD;
(2)求∠ACB的大小.

参考答案:
【答案】(1)证明见解析;(2)∠ACB=90°.
【解析】试题分析:(1)由两边对应成比例且夹角相等的两个三角形相似,即可证明△ACD∽△CBD;
(2)由(1)知△ACD∽△CBD,然后根据相似三角形的对应角相等可得:∠A=∠BCD,然后由∠A+∠ACD=90°,可得:∠BCD+∠ACD=90°,即∠ACB=90°.
试题解析:(1)∵CD是边AB上的高,
∴∠ADC=∠CDB=90°,
∵![]() .
.
∴△ACD∽△CBD;
(2)∵△ACD∽△CBD,
∴∠A=∠BCD,
在△ACD中,∠ADC=90°,
∴∠A+∠ACD=90°,
∴∠BCD+∠ACD=90°,
即∠ACB=90°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:﹣3x6+2x6的结果是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】王老师为了了解所教班级学生自主学习、合作交流的具体情况,对本班部分学生进行了为期半个月的跟踪调查,并将调查结果分成四类,A:优秀;B:良好;C:合格;D:一般;并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:

(1)本次调查中,王老师一共调查了 名同学,其中C类女生有 名,D类男生有 名;
(2)将上面的条形统计图补充完整;
(3)从被调查的A类和D类学生中分别选取一位同学进行“一对一”互助学习,请求出所选两位同学恰好是一位男同学和一位女同学的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠ACB=90°
(1)tanA与sinA,cosA之间有什么关系?并说明理由.
(2)若
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数y=kx+b的图象交反比例函数
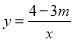 (x>0)图象于点A、B,交x轴于点C.
(x>0)图象于点A、B,交x轴于点C.(1)求m得取值范围;
(2)若点A的坐标是(2,﹣4),且
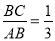 ,求m的值和一次函数的解析式.
,求m的值和一次函数的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】近似数2.30万精确到位,用科学记数法表为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】
如图,△ABC中,DE∥BC,AD:DB=1:2,下列选项正确的是( )
A.DE:BC=1:2
B.AE:AC=1:3
C.BD:AB=1:3
D.S△ADE:S△ABC=1:4
相关试题

