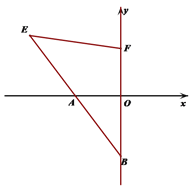
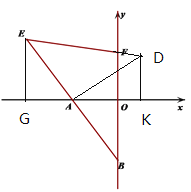
【题目】已知,如图A在x轴负半轴上,B(0,-4),点E(-6,4)在射线BA上,
(1) 求证:点A为BE的中点
(2) 在y轴正半轴上有一点F, 使 ∠FEA=45°,求点F的坐标.
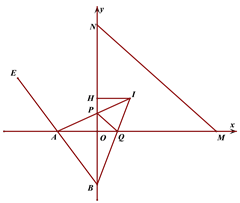
(3) 如图,点M、N分别在x轴正半轴、y轴正半轴上,MN=NB=MA,点I为△MON的内角平分线的交点,AI、BI分别交y轴正半轴、x轴正半轴于P、Q两点, IH⊥ON于H, 记△POQ的周长为C△POQ.求证:C△POQ=2 HI.
参考答案:
【答案】(1)证明见解析;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】试题分析:(1)过E点作EG⊥x轴于G,根据B、E点的坐标,可证明△AEG≌△ABO,从而根据全等三角形的性质得证;
(2)过A作AD⊥AE交EF延长线于D,过D作DK⊥x轴于K,然后根据全等三角形的判定得到△AEG≌△DAK,进而求出D点的坐标,然后设F坐标为(0,y),根据S梯形EGKD=S梯形EGOF+S梯形FOKD可求出F的坐标;
(3)连接MI、NI,根据全等三角形的判定SAS证得△MIN≌△MIA,从而得到∠MIN=∠MIA和∠MIN=∠NIB,由角平分线的性质,求得∠AIB=135°×3-360°=45°再连接OI,作IS⊥OM于S, 再次证明△HIP≌△SIC和△QIP≌△QIC,得到C△POQ周长.
试题解析:(1)过E点作EG⊥x轴于G,
∵B(0,-4),E(-6,4),∴OB=EG=4,
在△AEG和△ABO中,
∵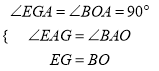
∴△AEG≌△ABO(AAS),∴AE=AB
∴A为BE中点
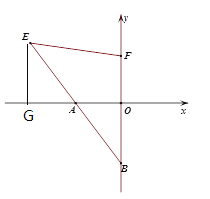
(2)过A作AD⊥AE交EF延长线于D,
过D作DK⊥x轴于K,
∵∠FEA=45°,∴AE=AD,
∴可证△AEG≌△DAK,∴D(1,3),
设F(0,y),
∵S梯形EGKD=S梯形EGOF+S梯形FOKD,
∴![]()
∴![]()
∴![]()
(3)连接MI、NI
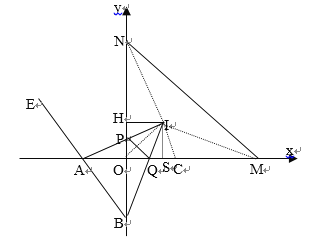
∵I为△MON内角平分线交点,
∴NI平分∠MNO,MI平分∠OMN,
在△MIN和△MIA中,
∵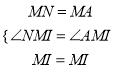
∴△MIN≌△MIA(SAS),
∴∠MIN=∠MIA,
同理可得∠MIN=∠NIB,
∵NI平分∠MNO,MI平分∠OMN,∠MON=90°,
∴∠MIN=135°∴∠MIN=∠MIA =∠NIB=135°,
∴∠AIB=135°×3-360°=45°,
连接OI,作IS⊥OM于S, ∵IH⊥ON,OI平分∠MON,
∴IH=IS=OH=OS,∠HIS=90°,∠HIP+∠QIS=45°,
在SM上截取SC=HP,可证△HIP≌△SIC,∴IP=IC,
∠HIP=∠SIC,∴∠QIC=45°,
可证△QIP≌△QIC,
∴PQ=QC=QS+HP,
∴C△POQ=OP+PQ+OQ=OP+PH+OQ+OS=OH+OS=2HI.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某饮料瓶上有这样的字样,保质期18个月.如果用x(单位:月)表示保质期,那么该饮料的保质期可以用不等式表示为________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的大小关系,并对结论进行说理.
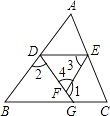
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个三角形的两边长是3和4,第三边的长是方程x2﹣6x+5=0的一个根,则该三角形的周长是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC和△ADE中,AB=AD,AC=AE, ∠BAC=∠DAE,BC交
DE于点O,∠BAD=a.
(1)求证:∠BOD=a.
(2)若AO平分∠DAC, 求证:AC=AD.
(3)若∠C=30°,OE交AC于F,且△AOF为等腰三角形,则a= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.2a+a=2a2
B.(﹣a)2=﹣a2
C.(a2)3=a5
D.a3÷a=a2 -
科目: 来源: 题型:
查看答案和解析>>【题目】至少有两边相等的三角形是( )
A. 等边三角形 B. 等腰三角形 C. 等腰直角三角形 D. 锐角三角形
相关试题

