【题目】如图所示,已知∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的大小关系,并对结论进行说理. 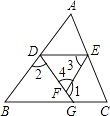
参考答案:
【答案】证明:∵∠1+∠4=180°(邻补角定义) ∠1+∠2=180°(已知)
∴∠2=∠4(同角的补角相等)
∴EF∥AB(内错角相等,两直线平行)
∴∠3=∠ADE(两直线平行,内错角相等)
又∵∠B=∠3(已知),
∴∠ADE=∠B(等量代换),
∴DE∥BC(同位角相等,两直线平行)
∴∠AED=∠C(两直线平行,同位角相等)
【解析】由图中题意可先猜测∠AED=∠C,那么需证明DE∥BC.题中说∠1+∠2=180°,而∠1+∠4=180°所以∠2=∠4,那么可得到BD∥EF,题中有∠3=∠B,所以应根据平行得到∠3与∠ADE之间的关系为相等.就得到了∠B与∠ADE之间的关系为相等,那么DE∥BC.
【考点精析】认真审题,首先需要了解平行线的性质(两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是()
A.a4+a2=a6B.a6÷a2=a3C.a2a3=a6D.(﹣2ab2)3=﹣8a3b6
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=(x﹣1)2+2的顶点坐标是( )
A.(1,2)B.(1,﹣2)C.(﹣1,2)D.(﹣1,﹣2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某饮料瓶上有这样的字样,保质期18个月.如果用x(单位:月)表示保质期,那么该饮料的保质期可以用不等式表示为________
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个三角形的两边长是3和4,第三边的长是方程x2﹣6x+5=0的一个根,则该三角形的周长是_____.
-
科目: 来源: 题型:
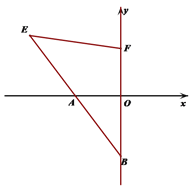
查看答案和解析>>【题目】已知,如图A在x轴负半轴上,B(0,-4),点E(-6,4)在射线BA上,
(1) 求证:点A为BE的中点
(2) 在y轴正半轴上有一点F, 使 ∠FEA=45°,求点F的坐标.
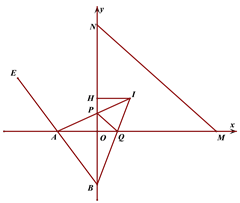
(3) 如图,点M、N分别在x轴正半轴、y轴正半轴上,MN=NB=MA,点I为△MON的内角平分线的交点,AI、BI分别交y轴正半轴、x轴正半轴于P、Q两点, IH⊥ON于H, 记△POQ的周长为C△POQ.求证:C△POQ=2 HI.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC和△ADE中,AB=AD,AC=AE, ∠BAC=∠DAE,BC交
DE于点O,∠BAD=a.
(1)求证:∠BOD=a.
(2)若AO平分∠DAC, 求证:AC=AD.
(3)若∠C=30°,OE交AC于F,且△AOF为等腰三角形,则a= .

相关试题

