搜索
【题目】夏师傅是一名徒步运动的爱好者，他用手机软件记录了某个月（30天）每天徒步的步数（单位：万步），将记录结果绘制成了如图所示的统计图．在这组徒步数据中，众数和中位数分别是（ ）
A. 1.2，1.3 B. 1.4，1.3 C. 1.4，1.35 D. 1.3，1.3
参考答案：
【答案】B
【解析】分析：中位数是将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（最中间两个数的平均数），众数是一组数据中出现次数最多的数据，据此判断即可．
详解：∵这组数据中1.4出现的次数最多，∴在每天所走的步数这组数据中，众数是1.4；
每天所走的步数的中位数是：
（1.3+1.3）÷2=1.3
∴在每天所走的步数这组数据中，众数和中位数分别是1.4、1.3．
故选B．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知数
，
表示的点在数轴上的位置如图所示.
(1)在数轴上表示出
，的相反数的位置；(2)若数
与其相反数相距20个单位长度，则表示的数是多少？(3)在(2)的条件下，若数
表示的点与数的相反数表示的点相距5个单位长度，求表示的数是多少？ -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，边长为3的正方形OABC的两边在两坐标轴上，抛物线y＝－x2＋bx＋c经过点A，C，与x轴交于另一点D，P为第一象限内抛物线上一点，过P点作y轴的平行线交x 轴于点Q，交AC于点E.
(1)求抛物线解析式及点D的坐标；
(2)过E点作x轴的平行线交AB于点F，若以P，E，F为顶点的三角形与△ODC相似，求点P坐标；
(3)过P点作PH⊥AC于H，是否存在点P使△PEH的周长取得最大值，若存在，请求出点P坐标及△PEH周长的最大值，若不存在，请说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）如图①，△ABC中，∠ABC、∠ACB的平分线交于O点，过O点作EF∥BC交AB、AC于点E、F．试猜想EF、BE、CF之间有怎样的关系，并说明理由.
（2）如图，若将图①中∠ACB的平分线改为外角∠ACD的平分线，其它条件不变，则刚才的结论还成立吗？请说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，点
为直线AB上一点，过O点作射线
，使
，将一直角三角板的直角顶点放在点处，一边OM在射线OB上，另一边ON在直线AB的下方.(1)将图1中的三角板绕点
按逆时针方向旋转至图2的位置，使得ON落在射线OB上，此时三角板旋转的角度为_______度.
(2)继续将图2中的三角板绕点
按逆时针方向旋转至图3的位置，使得ON在
的内部.试探究
与
之间满足什么等量关系，并说明理由；(3)在上述直角三角板从图1开始绕点O按
每秒的速度逆时针旋转
的过程中， 是否存在
所在直线平分
和中的一个角，ON所在直线平分另一个角？若存在，直接写出旋转时间
，若不存在，说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点O是边长为
的等边△ABC的内心，将△OBC绕点O逆时针旋转30°得到△OB1C1，B1C1交BC于点D，B1C1交AC于点E，则CE=( )
A. 2 B.
C. 
D.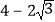 
-
科目： 来源： 题型：
查看答案和解析>>【题目】某报社为了解市民对“社会主义核心价值观”的知晓程度，采取随机抽样的方式进行问卷调查，调查结果分为“A.非常了解”、“B.了解”、“C.基本了解”三个等级，并根据调查结果绘制了如下两幅不完整的统计图．
(1)这次调查的市民人数为________人，m＝________，n＝________；
(2)补全条形统计图；
(3)若该市约有市民100000人，请你根据抽样调查的结果，估计该市大约有多少人对“社会主义核心价值观”达到“A.非常了解”的程度．
相关试题
