【题目】如图,在□ABCD中,点E是CD的中点,点F是BC边上的一点,且EF⊥AE.求证:AE平分∠DAF.
小林同学读题后有一个想法,延长FE,AD交于点M,要证AE平分∠DAF,只需证△AMF是等腰三角形即可.请你参考小林的想法,完成此题的证明.
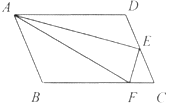
参考答案:
【答案】证明见解析.
【解析】延长FE,AD交于点M,要证AE平分∠DAF,只需证△AMF是等腰三角形即可.
证明:延长AD,FE交于M.

在□ABCD中,AD∥BC,
所以∠MDE=∠FCE,∠EMD=∠EFC,
又E是CD的中点,所以DE= CE,
所以△EDM≌△ECF,
所以EM= EF.
又因为EF⊥AE,
所以AF=AM,即△AMF是等腰三角形,
又AE⊥FM,所以AE平分∠DAF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,⊙O的半径是5cm,PA、PB切⊙O于点A、B两点,∠PAB=60°.求AB的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=15,AC=13,BC边上的高AD=12,则BC的长为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】石头剪子布,又称“猜丁壳”,是一种起源于中国流传多年的猜拳游戏.游戏时的各方每次用一只手做“石头”、“剪刀”、“布”三种手势中的一种,规定“石头”胜“剪刀”、“剪刀”胜“布”、“布”胜“石头”.两人游戏时,若出现相同手势,则不分胜负游戏继续,直到分出胜负,游戏结束.三人游戏时,若三种手势都相同或都不相同,则不分胜负游戏继续;若出现两人手势相同,则视为一种手势与第三人所出手势进行对决,此时,参照两人游戏规则.例如甲、乙二人同时出石头,丙出剪刀,则甲、乙获胜.假定甲、乙、丙三人每次都是随机地做这三种手势,那么:
(1)请你用画树状图或列表的方式,求出一次游戏中甲、乙两人出第一次手势时,不分胜负的概率;
(2)请直接写出一次游戏中甲、乙、丙三人出第一次手势时,不分胜负的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平行四边形ABCD中,E是AD上一点,AE=AB,过点E作直线EF,在EF上取一点G,使得∠EGB=∠EAB,连接AG.
(1)如图①,当EF与AB相交时,若∠EAB=60°,求证:EG=AG+BG;
(2)如图②,当EF与CD相交时,且∠EAB=90°,请你写出线段EG、AG、BG之间的数量关系,并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:△ABC是⊙O的内接三角形,∠ACB=45°,∠AOC=150°,过点C作⊙O的切线交AB的延长线于点D.

(1)求证:CD=CB;
(2)如果⊙O的半径为 ,求AB的长.
,求AB的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】某篮球运动员去年共参加
 场比赛,其中
场比赛,其中 分球的命中率为
分球的命中率为 ,平均每场有
,平均每场有 次
次 分球未投中.
分球未投中. 该运动员去年的比赛中共投中多少个
该运动员去年的比赛中共投中多少个 分球?
分球? 在其中的一场比赛中,该运动员
在其中的一场比赛中,该运动员 分球共出手
分球共出手 次,小明说,该运动员这场比赛中一定投中了
次,小明说,该运动员这场比赛中一定投中了 个
个 分球,你认为小明的说法正确吗?请说明理由.
分球,你认为小明的说法正确吗?请说明理由.
相关试题

