【题目】甲、乙两人利用扑克牌玩“10点”游戏，游戏规则如下：

①将牌面数字作为“点数”，如红桃6的“点数”就是6（牌面点数与牌的花色无关）；

②两人摸牌结束时，将所得牌的“点数”相加，若“点数”之和小于或等于10，此时“点数”之和就是“最终点数”，若“点数”之和大于10，则“最终点数”是0；

③游戏结束之前双方均不知道对方“点数”；

④判定游戏结果的依据是：“最终点数”大的一方获胜，“最终点数”相等时不分胜负．

现甲、乙均各自摸了两张牌，数字之和都是5，这时桌上还有四张背面朝上的扑克牌，牌面数字分别是4，5，6，7．

（1）若甲从桌上继续摸一张扑克牌，乙不再摸牌，则甲获胜的概率为 ；

（2）若甲先从桌上继续摸一张扑克牌，接着乙从剩下的扑克牌中摸出一张牌，然后双方不再摸牌，请用树状图或表格表示出这次摸牌后所有可能的结果，再列表呈现甲、乙的“最终点数”，并求乙获胜的概率．

参考答案：

【答案】（1）；（2）．

【解析】试题分析：（1）甲摸到4或5可获胜，摸到6和7则乙获胜，即可得到甲获胜的概率；

（2）画出树状图，即可得出结论．

试题解析：（1）甲摸到4或5可获胜，摸到6和7则乙获胜，∴P（甲获胜）==．

（2）如图：

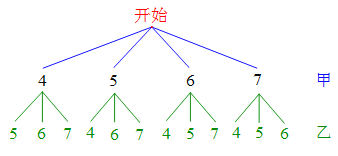
∴所有可能的结果是（4，5）（4，6）（4，7）（5，4）（5，6）（5，7）（6，4）（6，5）（6，7）

（7，4）（7，5）（7，6） 共12种．

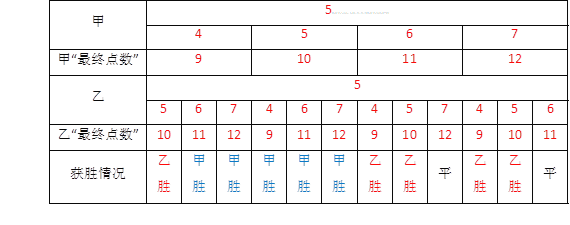
∴P（乙获胜）=．

关闭