【题目】在平面直角坐标系xOy中,直线l1:y=k1x+b过A(0,﹣3),B(5,2),直线l2:y=k2x+2. 
(1)求直线l1的表达式;
(2)当x≥4时,不等式k1x+b>k2x+2恒成立,请写出一个满足题意的k2的值.
参考答案:
【答案】
(1)解:∵直线l1:y=k1x+b过A(0,﹣3),B(5,2),
∴ ![]() ,解得
,解得 ![]() ,
,
∴直线l1的表达式为y=x﹣3
(2)解:∵当x≥4时,不等式x﹣3>k2x+2恒成立,
∴4﹣3>4k2+2,
∴k2<﹣ ![]() ,
,
∴取k2=﹣1满足题意
【解析】(1)把A(0,﹣3),B(5,2)代入y=k1x+b,利用待定系数法即可求出直线l1的表达式;(2)根据题意,把x=4代入k1x+b>k2x+2,求出k2的范围,进而求解即可.
【考点精析】解答此题的关键在于理解确定一次函数的表达式的相关知识,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(
 )﹣1+2cos45°+|
)﹣1+2cos45°+|  ﹣1|﹣(3.14﹣π)0 .
﹣1|﹣(3.14﹣π)0 . -
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式3(x﹣1)≤
 ,并把它的解集在数轴上表示出来.
,并把它的解集在数轴上表示出来. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边三角形ABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AC边上一点.若AE=2,当EF+CF取得最小值时,∠ECF的度数为( )

A. 20° B. 25° C. 30° D. 45°
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级共有8个班,241名同学,历史老师为了了解新中考模式下该校八年级学生选修历史学科的意向,请小红,小亮,小军三位同学分别进行抽样调查.三位同学调查结果反馈如下:

小红、小亮和小军三人中,你认为哪位同学的调查结果较好地反映了该校八年级同学选修历史的意向,请说出理由,并由此估计全年级有意向选修历史的同学的人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,若∠A=15°,AB=BC=CD=DE=EF,则∠DEF等于__________.
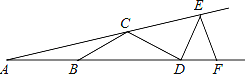
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AE⊥BC于点E点,延长BC至F点使CF=BE,连接AF,DE,DF.

(1)求证:四边形AEFD是矩形;
(2)若AB=6,DE=8,BF=10,求AE的长.
相关试题

