【题目】如图,有一个形如六边形的点阵,它的中心是一个点,算第一层,第二层每边有两个点,第三层每边有三个点,依此类推.

(1)填写下表;
层数 | 1 | 2 | 3 | 4 | 5 | … |
该层对应的点数 | 1 | 6 | __________ | __________ | __________ | … |
(2)写出第![]() 层所对应的点数;
层所对应的点数;
(3)是否存在![]() ,使得第
,使得第![]() 层有96个点?如果存在,求出
层有96个点?如果存在,求出![]() 的值;如果不存在,说明理由.
的值;如果不存在,说明理由.
参考答案:
【答案】(1)12;18;24;(2)6n-6;(3)存在;n=17
【解析】
(1)观察图形,分别求解即可;
(2)根据(1)所得出的规律是第几层就是第几个数乘以6,再减去6,即可求出答案;
(3)根据(2)所得的规律列出方程6n-6=96,求出n的值即可.
(1)由题意,得
第二层的六边形点阵的总点数2×6-6=6,
第三层的六边形点阵的总点数3×6-6=12,
第四层的六边形点阵的总点数4×6-6=18,
第五层的六边形点阵的总点数5×6-6=24,
故答案为:12;18;24;
(2)根据(1)所得的规律:
第n(n>1)层所对应的点数为6×n-6=6n-6;
(3)存在;
假设存在,则有6n-6=96,解得n=17.
-
科目: 来源: 题型:
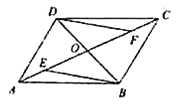
查看答案和解析>>【题目】如图,
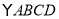 的对角线
的对角线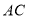 ,
,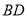 相交于点
相交于点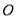 ,
,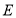 ,
,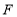 是
是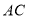 上的两点,并且
上的两点,并且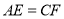 ,连接
,连接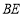 ,
,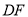 .
.
(1)求证
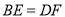 ;
;(2)若
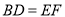 ,连接
,连接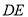 ,
,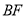 ,判断四边形
,判断四边形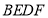 的形状,并说明理由.
的形状,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场新进一批商品,每个成本价25元,销售一段时间发现销售量y(个)与销售单价x(元/个)之间成一次函数关系,如下表:

(1)求y与x之间的函数关系式;
(2)若该商品的销售单价在45元~80元之间浮动,
①销售单价定为多少元时,销售利润最大?此时销售量为多少?
②商场想要在这段时间内获得4550元的销售利润,销售单价应定为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知线段
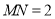 ,点
,点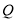 是线段
是线段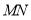 的中点,先按要求画图形,再解决问题.
的中点,先按要求画图形,再解决问题.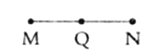
(1)延长线段
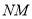 至点
至点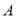 ,使
,使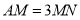 ;延长线段
;延长线段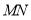 至点
至点 ,使
,使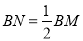 ;(尺规作图,保留作图痕迹)
;(尺规作图,保留作图痕迹)(2)求线段
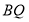 的长度;
的长度;(3)若点
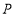 是线段
是线段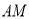 的中点,求线段
的中点,求线段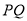 的长度.
的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】有两张完全重合的矩形纸片,小亮同学将其中一张绕点A顺时针旋转90°后得到矩形AMEF(如图1),连接BD、MF,若此时他测得BD=8cm,∠ADB=30度.请回答下列问题:(1)试探究线段BD与线段MF的关系,并简要说明理由;
(2)小红同学用剪刀将△BCD与△MEF剪去,与小亮同学继续探究.他们将△ABD绕点A顺时针旋转得△AB1D1,AD1交FM于点K(如图2),设旋转角为β(0°<β<90°),当△AFK为等腰三角形时,请直接写出旋转角β的度数;
(3)若将△AFM沿AB方向平移得到△A2F2M2(如图3),F2M2与AD交于点P,A2M2与BD交于点N,当NP∥AB时,求平移的距离是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,抛物线过原点O,点A(10,0)和点B(2,2),在线段OA上,点P从点O向点A运动,同时点Q从点A向点O运动,运动过程中保持AQ=2OP,当P、Q重合时同时停止运动,过点Q作x轴的垂线,交直线AB于点M,延长QM到点D,使MD=MQ,以QD为对角线作正方形QCDE(正方形QCDE随点Q运动).
(1)求这条抛物线的函数表达式;
(2)设正方形QCDE的面积为S,P点坐标(m,0)求S与m之间的函数关系式;
(3)过点P作x轴的垂线,交抛物线于点N,延长PN到点G,使NG=PN,以PG为对角线作正方形PFGH(正方形PFGH随点P运动),当点P运动到点(2,0)时,如图2,正方形PFGH的边GF和正方形QCDE的边EQ落在同一条直线上.
①则此时两个正方形中在直线AB下方的阴影部分面积的和是多少?
②若点P继续向点A运动,还存在两个正方形分别有边落在同一条直线上的情况,请直接写出每种情况下点P的坐标,不必说明理由.

-
科目: 来源: 题型:
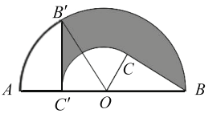
查看答案和解析>>【题目】如图,
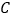 为半圆内一点,
为半圆内一点,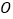 为圆心,直径
为圆心,直径 长为
长为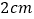 ,
,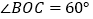 ,
,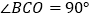 ,将
,将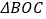 绕圆心
绕圆心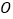 逆时针旋转至
逆时针旋转至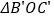 ,点
,点 在
在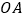 上,则边
上,则边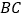 扫过区域(图中阴影部分)的面积为__________
扫过区域(图中阴影部分)的面积为__________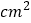 .(结果保留
.(结果保留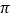 )
)
相关试题

