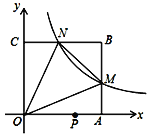
【题目】如图,在平面直角坐标系中,反比例函数![]() 的图像与边长是6的正方形
的图像与边长是6的正方形![]() 的两边
的两边![]() 分别相交于
分别相交于![]() 两点,
两点,![]() 的面积为10.若动点
的面积为10.若动点![]() 在
在![]() 轴上,则
轴上,则![]() 的最小值是_____________
的最小值是_____________
参考答案:
【答案】2![]()
【解析】由正方形OABC的边长是6,得到点M的横坐标和点N的纵坐标为6,求得M(6,![]() ),N(
),N(![]() ,6),根据三角形的面积列方程得到M(6,4),N(4,6),作M关于x轴的对称点M′,连接NM′交x轴于P,则NM′的长=PM+PN的最小值,根据勾股定理即可得到结论.
,6),根据三角形的面积列方程得到M(6,4),N(4,6),作M关于x轴的对称点M′,连接NM′交x轴于P,则NM′的长=PM+PN的最小值,根据勾股定理即可得到结论.
∵正方形OABC的边长是6,
∴点M的横坐标和点N的纵坐标为6,
∴M(6, ![]() ),N(
),N(![]() ,6),
,6),
∵△OMN的面积为10,
∴![]() ,
,
∴k=![]() ,
,
∵![]() ,
,
∴k=24,
∴M(6,4),N(4,6),
作M关于x轴的对称点M′,连接NM′交x轴于P,则M′N的长等于PM+PN的最小值,
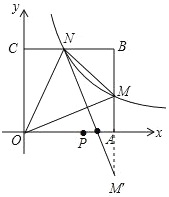
∵AB=6,M(6,4),N(4,6),
∴AM′=AM =4,BN=2,
∴BM′=10, BN=2,
根据勾股定理求得NM′=![]() .
.
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作⊙O的切线DF,交AC于点F.
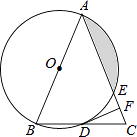
(1)求证:DF⊥AC;
(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果两个三角形的两条边对应相等,夹角互补,那么这两个三角形叫做互补三角形,如图2,分别以△ABC的边AB、AC为边向外作正方形ABDE和ACGF,则图中的两个三角形就是互补三角形.
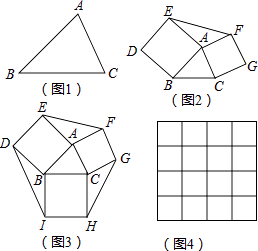
(1)图1中的△ABC的BC边上有一点D,线段AD将△ABC分成两个互补三角形,则点D在BC边的处.
(2)证明:图2中的△ABC分割成两个互补三角形面积相等;
(3)如图3,在图2的基础上再以BC为边向外作正方形BCHI,已知三个正方形面积分别是17、13、10.则图3中六边形DEFGHI的面积为 . (提示:可先利用图4求出△ABC的面积) -
科目: 来源: 题型:
查看答案和解析>>【题目】(2017怀化,第10题,4分)如图,A,B两点在反比例函数
 的图象上,C,D两点在反比例函数
的图象上,C,D两点在反比例函数 的图象上,AC⊥y轴于点E,BD⊥y轴于点F,AC=2,BD=1,EF=3,则
的图象上,AC⊥y轴于点E,BD⊥y轴于点F,AC=2,BD=1,EF=3,则 的值是( )
的值是( )
A. 6 B. 4 C. 3 D. 2
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两同学的家与学校的距离均为3000米.甲同学先步行600米,然后乘公交车去学校、乙同学骑自行车去学校.已知甲步行速度是乙骑自行车速度的
 ,公交车的速度是乙骑自行车速度的2倍.甲乙两同学同时从家发去学校,结果甲同学比乙同学早到2分钟.
,公交车的速度是乙骑自行车速度的2倍.甲乙两同学同时从家发去学校,结果甲同学比乙同学早到2分钟.(1)求乙骑自行车的速度;
(2)当甲到达学校时,乙同学离学校还有多远?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一家商店因换季将某种服装打折销售,如果每件服装按标价的5折出售将亏20元,而按标价的8折出售将赚40元.
问:(1)每件服装的标价、成本各是多少元?
(2)为了保证不亏损,最多可以打几折?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线经过点A(2,0)和B(t,0)(t≥2),与y轴交于点C,直线l:y=x+2t经过点C,交x轴于点D,直线AE交抛物线于点E,且有∠CAE=∠CDO,作CF⊥AE于点F.
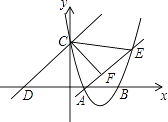
(1)求∠CDO的度数;
(2)求出点F坐标的表达式(用含t的代数式表示);
(3)当S△COD﹣S四边形COAF=7时,求抛物线解析式;
(4)当以B,C,O三点为顶点的三角形与△CEF相似时,请直接写出t的值.
相关试题

