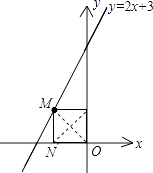
【题目】如图,点M是直线y=2x+3上的动点,过点M作MN垂直于x轴于点N,y轴上是否存在点P,使△MNP为等腰直角三角形,请写出符合条件的点P的坐标 . 
参考答案:
【答案】(0,0),(0,1),(0, ![]() ),(0,﹣3)
),(0,﹣3)
【解析】解:当M运动到(﹣1,1)时,ON=1,MN=1,
∵MN⊥x轴,所以由ON=MN可知,(0,0)和(0,1)就是符合条件的两个P点;
又∵当M运动到第三象限时,要MN=MP,且PM⊥MN,
设点M(x,2x+3),则有﹣x=﹣(2x+3),
解得x=﹣3,所以点P坐标为(0,﹣3).
如若MN为斜边时,则∠ONP=45°,所以ON=OP,设点M(x,2x+3),
则有﹣x=﹣ ![]() (2x+3),化简得﹣2x=﹣2x﹣3,
(2x+3),化简得﹣2x=﹣2x﹣3,
这方程无解,所以这时不存在符合条件的P点;
又∵当点M′在第二象限,M′N′为斜边时,这时N′P=M′P,∠M′N′P=45°,
设点M′(x,2x+3),则OP=ON′,而OP= ![]() M′N′,
M′N′,
∴有﹣x= ![]() (2x+3),
(2x+3),
解得x=﹣ ![]() ,这时点P的坐标为(0,
,这时点P的坐标为(0, ![]() ).
).
综上,符合条件的点P坐标是(0,0),(0, ![]() ),(0,﹣3),(0,1).
),(0,﹣3),(0,1).
所以答案是:(0,0),(0,1),(0, ![]() ),(0,﹣3).
),(0,﹣3).
【考点精析】本题主要考查了一次函数的性质和一次函数的图象和性质的相关知识点,需要掌握一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小;一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边三角形ACD及等边三角形ABE.已知∠BAC = 30,EF⊥AB于点 F,连接 DF.
(1)求证:AC=EF;
(2)求证:四边形 ADFE是平行四边形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a<﹣2,点(a﹣2,y1),(a,y2),(a+2,y3)都在函数y=﹣3x2+5的图象上,则y1,y2,y3的大小关系是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市计划争取“全面改薄”专项资金120 000 000元,用于改造农村义务教育薄弱学校100所数据120 000 000用科学记数法表示为( )
A. 12×108B. 1.2×108C. 1.2×109D. 0.12×109
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线
 与y轴交于点C,与x轴交于A,B两点(点A在点B左侧),且点A的横坐标为﹣1.
与y轴交于点C,与x轴交于A,B两点(点A在点B左侧),且点A的横坐标为﹣1.(1)求a的值;
(2)设抛物线的顶点P关于原点的对称点为P′,求点P′的坐标;
(3)将抛物线在A,B两点之间的部分(包括A,B两点),先向下平移 3个单位,再向左平移m(
 )个单位,平移后的图象记为图象G,若图象G与直线PP′ 无交点,求m的取值范围.
)个单位,平移后的图象记为图象G,若图象G与直线PP′ 无交点,求m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:
(1)(x+2)2-(x+5)(x-5),其中x=
 。
。(2)[(x+2y)2-(x+y)(3x-y)-5y2]÷2x,其中x=-2,y=
 。
。 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)求x的值:(x﹣1)2=25;
(2)计算: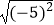 ﹣
﹣ 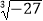 +
+ 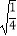 .
.
相关试题

