【题目】观察探究及应用.
(1)观察图形并填空:

一个四边形有________条对角线;
一个五边形有________条对角线;
一个六边形有________对角线;
一个七边形有________对角线;
(2)分析探究:
由凸n边形的一个顶点出发,可作_________条对角线,多边形有n个顶点,若允许重复计数,共可作_______条对角线;
(3)结论:
一个凸n边形有![]() 条对角线;
条对角线;
(4)应用:
一个凸十二边形有多少条对角线?
参考答案:
【答案】 2 5 9 14 (n-3) n(n-3)
【解析】试题分析:(1)根据图形数出对角线条数即可;
(2)根据n边形从一个顶点出发可引出(n﹣3)条对角线即可求解;
(3)由(2)可知,任意凸n边形的对角线有条![]() ,即可解答;
,即可解答;
(4)由(3)把n=12代入计算即可.
试题解析:解:(1)根据图形数出对角线条数,一个四边形有2条对角线,一个五边形有5条对角线,一个六边形有9对角线,一个七边形有14对角线;
故答案为:9;14.
(2)n边形从一个顶点出发可引出(n﹣3)条对角线,若允许重复计数,共可作n(n﹣3)条对角线;
故答案为:(n﹣3);n(n﹣3).
(3)由(2)可知,任意凸n边形的对角线有条![]() ,故答案为:
,故答案为: ![]() .
.
(4)把n=12代入![]() 计算得:
计算得: ![]() =54.
=54.
故答案为:54.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AD是BC边上的高,点E、F是AD的三等分点,若△ABC的面积为12cm2 , 则图中阴影部分的面积是cm2 .
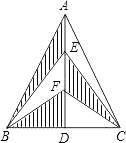
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图的方格纸中,每个小正方形的边长都为l,△ABC的顶点坐标分别为A(﹣4,4)、B(﹣2,3)、C(﹣3,1).

(1)在图中画出与△ABC关于y轴对称的△A1B1C1 , 并直接写出△A1B1C1的三个顶点坐标;
(2)画出将△A1B1C1向下平移4格得到的△A2B2C2 , 并直接写出△A2B2C2的三个顶点坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市6月上旬前5天的最高气温如下(单位:℃):28,29,31,29,32,对于这组数据,众数是_____,中位数是_____,极差是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 与x轴交点A(1,0),B(-3,0) .与y轴交点B(0,3),如图1所示,D为抛物线的顶点。
与x轴交点A(1,0),B(-3,0) .与y轴交点B(0,3),如图1所示,D为抛物线的顶点。(1)求抛物线的解析式;
(2)如图1若R为y轴上的一个动点,连接AR,则

 RB+AR的最小值为
RB+AR的最小值为 (3)在x轴上取一动点P(m,0),
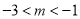 ,过点P作x轴的垂线,分别交抛物线、CD、CB于点Q、F、E,如图2所示,求证EF=EP.
,过点P作x轴的垂线,分别交抛物线、CD、CB于点Q、F、E,如图2所示,求证EF=EP.(4)设此抛物线的对称轴为直线MN,在直线MN上取一点T,使∠BTN=∠CTN.直接写出点T的坐标。

-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值
5(3a2b﹣ab2)﹣4(﹣ab2+3a2b),其中a=﹣2,b=3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(x2+y2)2-2(x2+y2)-3=0,则x2+y2=_____.
相关试题

