【题目】如图①,△ABC中, BD平分∠ABC , 且与△ABC的外角∠ACE的角平分线交于点D . 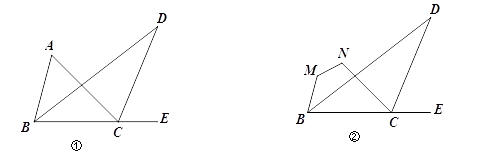
(1)若 ![]() ,
, ![]() ,求∠D的度数;
,求∠D的度数;
(2)若把∠A截去,得到四边形MNCB , 如图②,猜想∠D、∠M、∠N的关系,并说明理由.
参考答案:
【答案】
(1)解:∵BD平分∠ABC,
∴∠CBD= ![]() ∠ABC=
∠ABC= ![]() ×75°=37.5°,
×75°=37.5°,
∵CD平分△ABC的外角,
∴∠DCA= ![]() (180°-∠ACB)=
(180°-∠ACB)= ![]() (180°-45°)=67.5°,
(180°-45°)=67.5°,
∴∠D=180°-∠DBC-∠DCB=180°-37.5°-67.5°-45°=30°.
(2)解:猜想:∠ D = ![]() ( ∠ M + ∠ N 180 ° ).
( ∠ M + ∠ N 180 ° ).
∵∠M+∠N+∠CBM+∠NCB=360°,
∴∠D=180°- ![]() ∠CBM-∠NCB-
∠CBM-∠NCB- ![]() ∠NCE.
∠NCE.
=180°- ![]() (360°-∠NCB-∠M-∠N)- ∠NCB-
(360°-∠NCB-∠M-∠N)- ∠NCB- ![]() ∠NCE.
∠NCE.
=180°-180°+ ![]() ∠NCB+
∠NCB+ ![]() ∠M+
∠M+ ![]() ∠N-∠NCB-
∠N-∠NCB- ![]() ∠NCE.
∠NCE.
= ![]() ∠M+
∠M+ ![]() ∠N-
∠N- ![]() ∠NCB-
∠NCB- ![]() ∠NCE=
∠NCE= ![]() ,
,
或写成 ![]()
【解析】(1)根据角平分线的定义可得∠DBC=37.5°,根据邻补角定义以及角平分线定义求得∠DCA的度数为67.5°,最后根据三角形内角和定理即可求得∠D的度数;
(2)由四边形内角和与角平分线性质即可求解.
【考点精析】根据题目的已知条件,利用角的平分线和对顶角和邻补角的相关知识可以得到问题的答案,需要掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;两直线相交形成的四个角中,每一个角的邻补角有两个,而对顶角只有一个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:2﹣3= .
-
科目: 来源: 题型:
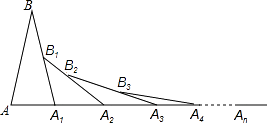
查看答案和解析>>【题目】如图,已知AB=A1B,A1B1=A1B2 , A2B2=A2B3 , A3B3=A3B4 , …若∠A=70°,则∠An的度数为( )
A.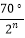
B.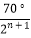
C.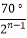
D.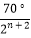
-
科目: 来源: 题型:
查看答案和解析>>【题目】若顺次连接四边形ABCD各边的中点所得四边形是矩形,则四边形ABCD一定满足( )
A.对角线相等
B.对角线互相平分
C.对角线互相垂直
D.对角线相等且相互平分 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于
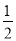 BF长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.
BF长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.(1)四边形ABEF是 ;(选填矩形、菱形、正方形、无法确定)(直接填写结果)
(2)AE,BF相交于点O,若四边形ABEF的周长为40,BF=10,则AE的长为 ,∠ABC= °.(直接填写结果)
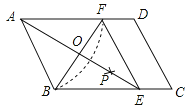
-
科目: 来源: 题型:
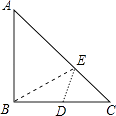
查看答案和解析>>【题目】如图,在Rt△ABC中,AB=BC=4,D为BC的中点,在AC边上存在一点E,连接ED,EB,则△BDE周长的最小值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A,B的坐标分别为A(a,b)、B(c,d),其中a>c,把点A 向上平移2单位,向左平移1个单位得点A1 .
(1)点A1的坐标为 .
(2)若a,b,c满足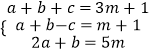 ,请用含m的式子表示a,b,c.
,请用含m的式子表示a,b,c.
(3)在(2)的前提下,若点A、B在第一象限或坐标轴的正半轴上,S 的面积是否存在最大值或最小值,如果存在,请求出这个值.如果不存在,请说明理由.
的面积是否存在最大值或最小值,如果存在,请求出这个值.如果不存在,请说明理由.
相关试题

