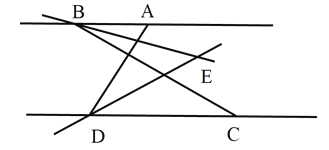
【题目】AB∥CD,C在 D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在的直线交于点 E.∠ADC=70°.
(1)求∠EDC 的度数;
(2)若∠ABC=30°,求∠BED 的度数;
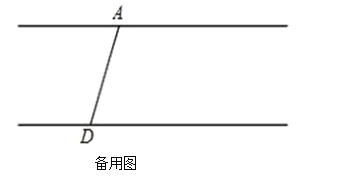
(3)将线段 BC沿 DC方向移动,使得点 B在点 A的右侧,其他条件不变,若∠ABC=n°,请直接写出∠BED 的度数(用含 n的代数式表示).
参考答案:
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)根据角平分线定义即可得到答案;
(2)过点![]() 作
作![]() ,然后根据角平分线的定义、平行线的判定和性质以及角的和差进行推导即可得解;
,然后根据角平分线的定义、平行线的判定和性质以及角的和差进行推导即可得解;
(3)过点![]() 作
作![]() ,然后根据角平分线的定义、平行线的判定和性质以及角的和差进行推导即可得解.
,然后根据角平分线的定义、平行线的判定和性质以及角的和差进行推导即可得解.
解:(1)∵![]() 平分
平分![]() ,
,![]()
∴![]() ;
;
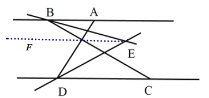
(2)过点![]() 作
作![]() ,如图:
,如图:
∵![]() 平分
平分![]() ,
,![]() ;
;![]() 平分
平分![]() ,
,![]()
∴![]() ,
,![]()
∵![]() ,
,![]()
∴![]()
∴![]() ,
,![]()
∴![]() ;
;
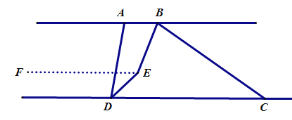
(3)过点![]() 作
作![]() ,如图:
,如图:
∵![]() 平分
平分![]() ,
,![]() ;
;![]() 平分
平分![]() ,
,![]()
∴![]() ,
,![]()
∵![]() ,
,![]()
∴![]()
∴![]() ,
,![]()
∴![]() .
.
故答案是:(1)![]() (2)
(2)![]() (3)
(3)![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一枚均匀的正方体骰子,骰子各个面上的点数分别为1,2,3,4,5,6,若任意抛掷一次骰子,朝上的面的点数记为x,计算|x﹣3|,则其结果恰为1的概率是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明骑单车上学,当他骑了一段路时,想起要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校.以下是他本次上学所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是 米.
(2)小明在书店停留了 分钟.
(3)本次上学途中,小明一共行驶了 米.一共用了 分钟.
(4)我们认为骑单车的速度超过 300 米/分就超过了安全限度.问:在整个上学途中哪个时间段小明的骑车速度最快,最快速度为多少,在安全限度内吗?

-
科目: 来源: 题型:
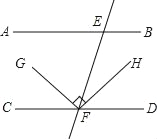
查看答案和解析>>【题目】如图,已知直线AB∥CD,FH平分∠EFD,FG⊥FH,∠AEF=62°,则∠GFC=_____度.
-
科目: 来源: 题型:
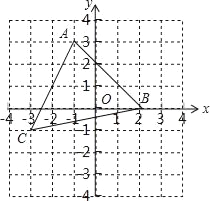
查看答案和解析>>【题目】如图,在平面直角坐标系中有一个△ABC,顶点A(﹣1,3),B(2,0),C(﹣3,﹣1).
(1)画出△ABC关于y轴的对称图形△A1B1C1(不写画法);
点A关于x轴对称的点坐标为
点B关于y轴对称的点坐标为
点C关于原点对称的点坐标为
(2)若网格上的每个小正方形的边长为1,则△ABC的面积是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,CD是AB边上的高,AC=4,BC=3,DB=


求:(1)求AD的长;
(2)△ABC是直角三角形吗?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式:
 ,
, ,
, ,
, ,…,则第8个等式是__________.
,…,则第8个等式是__________.
相关试题

