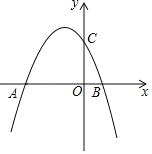
【题目】如图,已知抛物线y=-![]() x2+bx+6与x轴交于点A(﹣6,0)和点B,与y轴交于点C.
x2+bx+6与x轴交于点A(﹣6,0)和点B,与y轴交于点C.
(1)求该抛物线的解析式;
(2)写出顶点的坐标,并求AB的长;
(3)若点A,O,C均在⊙D上,请写出点D的坐标,连接BC,并判断直线BC与⊙D的位置关系.
参考答案:
【答案】(1)抛物线的解析式为y=﹣![]() x2﹣x+6;
x2﹣x+6;
(2)AB的长为9;
(3)D点的坐标为(﹣3,3),直线BC与⊙D相交.
【解析】试题分析:(1)根据待定系数法,可得答案;
(2)根据配方法,可得顶点坐标;根据自变量与函数值的对应关系,可得B点坐标,根据两点间的距离,可得答案;
(3)根据直角三角形的斜边大于直角边,可得r与d的关系,根据d<r,可得答案.
试题解析:
(1)将A点坐标代入函数解析式,得
﹣![]() ×(﹣6)﹣6b+6=0,
×(﹣6)﹣6b+6=0,
解得b=﹣1,
该抛物线的解析式为y=﹣![]() x2﹣x+6;
x2﹣x+6;
(2)y=﹣![]() x2﹣x+6配方,得
x2﹣x+6配方,得
y=﹣![]() (x+
(x+![]() )2+
)2+![]() ,
,
顶点坐标为(﹣![]() ,
, ![]() );
);
当y=0时,﹣![]() x2﹣x+6=0,
x2﹣x+6=0,
解得x=﹣6,x=3,
即A(﹣6,0)B(3,0),
AB的长3﹣(﹣6)=9;
AB的长为9;
(3)点D在AO的中垂线上,CO的中垂线上,
D点的横坐标为![]() =﹣3,D的纵坐标为
=﹣3,D的纵坐标为![]() =3,
=3,
D点的坐标为(﹣3,3);
作DE⊥BC于E如图,
DC>DE,
d>r,
直线BC与⊙D相交.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于命题“已知:a∥b,b∥c,求证:a∥c”.如果用反证法,应先假设( )
A. a不平行b B. b不平行c C. a⊥c D. a不平行c
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A(3,﹣1)关于原点的对称点A′的坐标是( )
A.(﹣3,﹣1)
B.(3,1)
C.(﹣3,1)
D.(﹣1,3) -
科目: 来源: 题型:
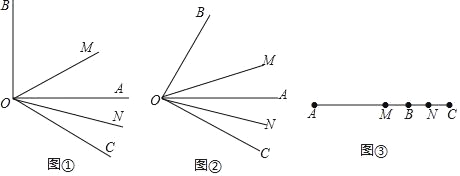
查看答案和解析>>【题目】理解计算:如图①,∠AOB=90°,∠AOC为∠AOB外的一个角,且∠AOC=30°,射线OM平分∠BOC,ON平分∠AOC.求∠MON的度数;
拓展探究:如图②,∠AOB=α,∠AOC=β.(α,β为锐角),射线OM平分∠BOC,ON平分∠AOC.求∠MON的度数;
迁移应用:其实线段的计算与角的计算存在着紧密的联系,如图③线段AB=m,延长线段AB到C,使得BC=n,点M,N分别为AC,BC的中点,则MN的长为_____(直接写出结果).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD为△ABC的中线,BE为三角形ABD中线.
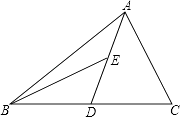
(1)在△BED中作BD边上的高EF;
(2)若△ABC的面积为40,BD=5,求EF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC的三个顶点的坐标分别为A(﹣5,3)、B(﹣2,﹣2)、C(﹣3,4).
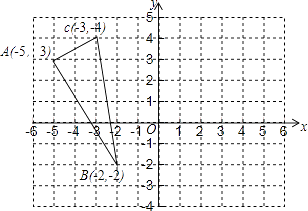
(1)作出△ABC关于y轴对称的△A1B1C1;
(2)写出点A关于x轴对称的点A2的坐标;
(3)△ABC的面积为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在平面直角坐标系中,已知A(3,4),B(3,﹣1),C(﹣3,﹣2),D(﹣2,3).
(1)在图上画出四边形ABCD,并求四边形ABCD的面积;
(2)若P为四边形ABCD形内一点,已知P坐标为(﹣1,1),将四边形ABCD通过平移后,P的坐标变为(2,﹣2),根据平移的规则,请直接写出四边形ABCD平移后的四个顶点的坐标.
相关试题

