搜索
【题目】如图，AD为△ABC的中线，BE为三角形ABD中线．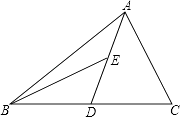 
（1）在△BED中作BD边上的高EF；
（2）若△ABC的面积为40，BD=5，求EF的长．
参考答案：
【答案】
（1）解；如图所示：
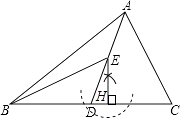
（2）解；∵AD为△ABC的中线，BE为三角形ABD中线，
∴S△ABD= 
S△ABC，S△BDE= S△ABD，
∴S△BDE= 
S△ABC，
∵△ABC的面积为40，BD=5，
∴ ×5×EF=10，
∴EF=4
【解析】（1）根据过直线外一点作已知直线的垂线的方法作图即可；（2）利用三角形中线的性质得出S△BDE= S△ABC ， 进而借助三角形面积公式求出即可．
【考点精析】掌握三角形的面积是解答本题的根本，需要知道三角形的面积=1/2×底×高．
-
科目： 来源： 题型：
查看答案和解析>>【题目】点A（3，﹣1）关于原点的对称点A′的坐标是（ ）
A.（﹣3，﹣1）
B.（3，1）
C.（﹣3，1）
D.（﹣1，3） -
科目： 来源： 题型：
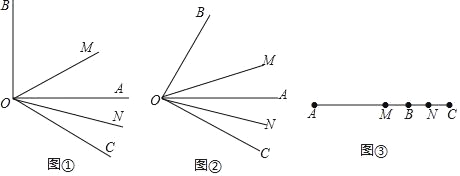
查看答案和解析>>【题目】理解计算：如图①，∠AOB=90°，∠AOC为∠AOB外的一个角，且∠AOC=30°，射线OM平分∠BOC，ON平分∠AOC．求∠MON的度数；
拓展探究：如图②，∠AOB=α，∠AOC=β．（α，β为锐角），射线OM平分∠BOC，ON平分∠AOC．求∠MON的度数；
迁移应用：其实线段的计算与角的计算存在着紧密的联系，如图③线段AB=m，延长线段AB到C，使得BC=n，点M，N分别为AC，BC的中点，则MN的长为_____（直接写出结果）．
-
科目： 来源： 题型：
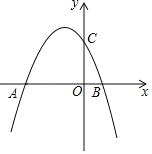
查看答案和解析>>【题目】如图，已知抛物线y=-
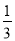x2+bx+6与x轴交于点A（﹣6，0）和点B，与y轴交于点C．（1）求该抛物线的解析式；
（2）写出顶点的坐标，并求AB的长；
（3）若点A，O，C均在⊙D上，请写出点D的坐标，连接BC，并判断直线BC与⊙D的位置关系．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知△ABC的三个顶点的坐标分别为A（﹣5，3）、B（﹣2，﹣2）、C（﹣3，4）．
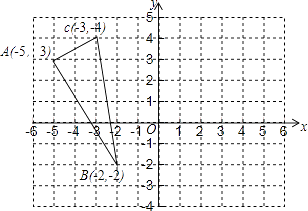
（1）作出△ABC关于y轴对称的△A1B1C1；
（2）写出点A关于x轴对称的点A2的坐标；
（3）△ABC的面积为 ． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知在平面直角坐标系中，已知A（3，4），B（3，﹣1），C（﹣3，﹣2），D（﹣2，3）.
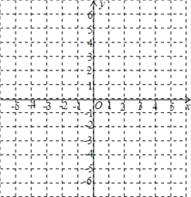
（1）在图上画出四边形ABCD，并求四边形ABCD的面积；
（2）若P为四边形ABCD形内一点，已知P坐标为（﹣1，1），将四边形ABCD通过平移后，P的坐标变为（2，﹣2），根据平移的规则，请直接写出四边形ABCD平移后的四个顶点的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】水位上升3米，记为+3米，水位下降2米，记为_________米.
相关试题
