【题目】五一节,小丽独自一人去老家玩,家住在车站附近的姑姑到车站去接小丽.因为担心小丽下车后找不到路,姑姑一路小跑来到车站,结果客车晚点,休息一阵后,姑姑接到小丽,和小丽一起慢慢的走回了家.下列图象中,能反映以上过程中小丽姑姑离家的距离s与时间t的关系的大致图象是( )
A.
B.
C.
D.
参考答案:
【答案】A
【解析】解:姑姑在车站休息的一段时间,路程不随时间的变化而变化,因而这一段的图象应该平行于横轴;
姑姑一路小跑来到车站,这段是正比例函数关系,回家的过程是一次函数关系,且s岁t的增大而减小,因而B、D错误;
回家的过程比姑姑一路小跑来到车站的过程速度要慢,即s随t的变化要慢,因而图象要平缓,故A正确,C错误.
故选A.
【考点精析】掌握函数的图象是解答本题的根本,需要知道函数的图像是由直角坐标系中的一系列点组成;图像上每一点坐标(x,y)代表了函数的一对对应值,他的横坐标x表示自变量的某个值,纵坐标y表示与它对应的函数值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若△ABC的三边长a,b,c满足(a-b)2+|b-2|+(c2-8)2=0,则下列对此三角形的形状描述最确切的是( )
A. 等边三角形 B. 等腰三角形 C. 等腰直角三角形 D. 直角三角形
-
科目: 来源: 题型:
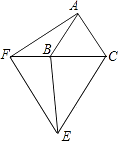
查看答案和解析>>【题目】如图,已知△ABC和△CEF是两个不等的等边三角形,且有一个公共顶点C,连接AF和BE,线段AF和BE有怎样的大小关系?证明你的猜想.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,设正方体ABCD-A1B1C1D1的棱长为1,黑甲壳虫从点A出发,白甲壳虫从点C1出发,它们以相同的速度分别沿棱向前爬行.黑甲壳虫爬行的路线是:AA1→A1D1→D1C1→C1C→CB→BA→AA1→A1D1…,白甲壳虫爬行的路线是:C1C→CB→BB1→B1C1→C1C→CB…,那么当黑、白两个甲壳虫各爬行完第2018条棱分别停止在所到的正方体顶点处时,它们之间的最短路程的平方是( )

A. 2 B. 3 C. 4 D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以平行四边形ABCO的顶点O为原点,边OC所在直线为x轴,建立平面直角坐标系,顶点A、C的坐标分别是(2,4)、(3,0),过点A的反比例函数y=
 的图象交BC于D,连接AD,则四边形AOCD的面积是( )
的图象交BC于D,连接AD,则四边形AOCD的面积是( ) 
A.6
B.7
C.9
D.10 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形纸片ABCD中,已知AD =8,折叠纸片使AB边与对角线AC
重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )

A. 3 B. 4
C. 5 D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】从﹣3,﹣2,﹣1,0,1,2这六个数字中随机抽取一个数,记为a,a的值即使得不等式组
 无解,又在函数y=
无解,又在函数y=  的自变量取值范围内的概率为 .
的自变量取值范围内的概率为 .
相关试题

