Question

【题目】如图1所示，在A，B两地之间有汽车站C站，客车由A地驶往C站，货车由B地驶往A地．两车同时出发，匀速行驶．图2是客车、货车离C站的路程y1 ， y2（千米）与行驶时间x（小时）之间的函数关系图象．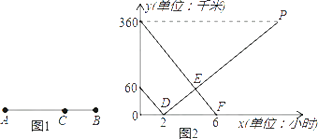

（1）填空：A ， B两地相距千米；
（2）求两小时后，货车离C站的路程y2与行驶时间x之间的函数关系式；
（3）客、货两车何时相遇？相遇处离C站的路程是多少千米？

Answer 1

【答案】
（1）420
（2）解:

（3）解:可求直线EF:

解得

答：客、货两车 小时相遇；相遇处离C站的路程是80千米

【解析】解：（1） 360+60=420（千米）；
（2）根据图像知货车由B到C行驶了两小时，BC两地相距60千米，
∴货车的平均速度为： 60÷2＝30(千米/小时) .
∴货车由C到A所用的事件为：360÷30=12（小时），
∴P（12,360）
设直线DP为y 2 = kx +b ,将（2,0）与（12,360）分别代入得
,
解得： '
∴两小时后，货车离C站的路程y2与行驶时间x之间的函数关系式: y 2 = 30 x 60 .

（1）由图像知AC=360KM ，BC=60KM ，故用AB=AC+BC算出答案；
（2）首先根据货车由B到C行驶了两小时，BC两地相距60千米，算出货车的速度，进而得出P点的坐标，然后利用待定系数法求出∴两小时后，货车离C站的路程y2与行驶时间x之间的函数关系式；
（3）首先算出直线EF的解析式，然后解 y 1 = 60 x + 360与 y 2 = 30 x 60 ，联立的方程组求出x,y的值，从而得出答案。