Question

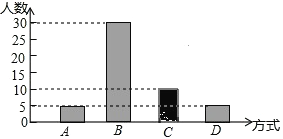
【题目】某班在一次班会课上，就“遇见路人摔倒后如何处理”的主题进行讨论，并对全班 50 名学生的处理方式进行统计，得出相关统计表和统计图．

组别	A	B	C	D
处理方式	迅速离开	马上救助	视情况而定	只看热闹
人数	m	30	n	5

请根据表图所提供的信息回答下列问题：

(1)统计表中的 m＝ ，n＝ ；

(2)补全频数分布直方图；

(3)若该校有 2000 名学生，请据此估计该校学生采取“马上救助”方式的学生有多少人？

Answer 1

【答案】(1)5，10；(2)补图见解析；(3)1200人.

【解析】

(1)根据条形统计图可以求得 m 的值，然后利用 50 减去其它各组的人数即可求得 n 的值；

(2)根据(1)的结果即可补全统计图；

(3)利用总人数 2000 乘以所占的比例即可求解．

(1)根据条形图可以得到：m＝5，n＝50﹣5﹣30﹣5＝10(人)，

故答案为：5，10；

(2)如图所示：

；

(3) 估计该校学生采取“马上救助”方式的学生有2000×＝1200(人)．