【题目】如图1,在平面直角坐标系中,将ABCD放置在第一象限,且AB∥x轴.直线y=﹣x从原点出发沿x轴正方向平移,在平移过程中直线被平行四边形截得的线段长度l与直线在x轴上平移的距离m的函数图象如图2所示,那么AD的长为 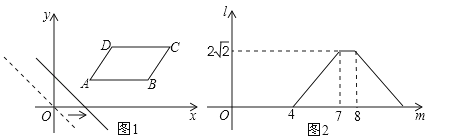
参考答案:
【答案】![]()
【解析】解:
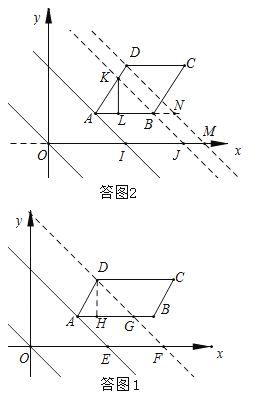
①先经过点D,即AB>3,如答图1:
设直线过点A时交x轴于点E,过点D交AB于点G,交x轴于点F,作DH⊥AB,
由图可知:OE=4,OF=7,DG=2![]() ,
,
∴EF=AG=OF﹣OE=3
∵直线y=﹣x
∴∠AGD=∠EFD=45°
∴△HGD是等腰直角三角形
∴DH=GH=![]() DG=
DG=![]() ×2
×2![]() =2
=2
∴AH=AG﹣GH=3﹣2=1
∴AD=![]()
②先经过点B,即AB=3,如答图2:
设直线过点A时交x轴于点I,过点B时交AD于点K、x轴于点J,过点D时,交AB延长线于点N、x轴于点M,并过K点作KL⊥AB,
由图可知:OI=4,OJ=7,KB=2![]() , OM=8,
, OM=8,
∴IJ=AB=3,IM=AN=4,
由直线y=﹣x,易得△KLB是等腰直角三角形,
∴KL=BL=![]() KB=
KB=![]() ×2
×2![]() =2,
=2,
∴AL=1,
∴AK=![]()
∵△ABK∽△AND,
∴![]() ,
,
即![]()
即AD=![]() .
. 
根据图象可以得到当移动的距离是4时,直线经过点A,当移动距离是7﹣8这段时,l的长度是不变的,可以得出直线是正好经过且在两条平行线 之间的,故此时需要分两种情况:①先经过点D,即AB>3,利用直线的性质得到△HGD是等腰直角三角形,从而求出DH、AH的值,再利用勾股定理解得 AD;②先经过点B,即AB=3,利用等腰直角三角形△KLB的性质得到AK的值,然后利用△ABK∽△AND,可得到AD的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
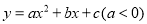 与双曲线
与双曲线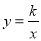 全相交于点A、B,且抛物线经过坐标原点,点
全相交于点A、B,且抛物线经过坐标原点,点 的坐标为(一2,2),点B在第四象限内.过点B作直线BC//x轴,点C为直线BC与抛物线的另一交点,已知直线BC与x轴之间的距离是点B到y轴的距离的4倍.记抛物线顶点为E.
的坐标为(一2,2),点B在第四象限内.过点B作直线BC//x轴,点C为直线BC与抛物线的另一交点,已知直线BC与x轴之间的距离是点B到y轴的距离的4倍.记抛物线顶点为E.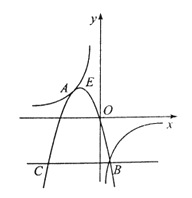
(1)求双曲线和抛物线的解析式;
(2)计算
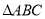 与
与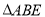 的面积;
的面积;(3)在抛物线上是否存在点D,使
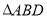 的面积等于
的面积等于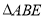 的面积的8倍?若存在,请求出点D的坐标;若不存在,请说明理由.
的面积的8倍?若存在,请求出点D的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列对数学符号|﹣2017|描述正确的是( )
A. 2017的相反数 B. ﹣2017的绝对值
C. ﹣2017的倒数 D. ﹣2017的相反数
-
科目: 来源: 题型:
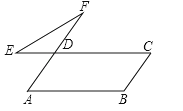
查看答案和解析>>【题目】如图,在平行四边形ABCD中,∠B=110°,延长AD至F,延长CD至E,连接EF,则∠E+∠F的值为度.
-
科目: 来源: 题型:
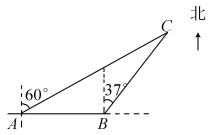
查看答案和解析>>【题目】一艘观光游船从港口A处以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发生了求救信号,一艘在港口正东方向B处的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里/时的速度前往救援,求海警船到达事故船C处所需的大约时间.(参考数据:sin53°≈0.8,cos53°≈0.6)
-
科目: 来源: 题型:
查看答案和解析>>【题目】用配方法解关于x的一元二次方程x2﹣2x﹣3=0,配方后的方程可以是( )
A.(x﹣1)2=4
B.(x+1)2=4
C.(x﹣1)2=16
D.(x+1)2=16 -
科目: 来源: 题型:
查看答案和解析>>【题目】袋中装有除颜色外完全相同的2个红球和1个绿球.
(1)现从袋中摸出1个球后放回,混合均匀后再摸出1个球.请用画树状图或列表的方法,求第一次摸到绿球,第二次摸到红球的概率;
(2)先从袋中摸出1个球后不放回,再摸出1个球,则两次摸到的球中有1个绿球和1个红球的概率是多少?请直接写出结果.
相关试题

