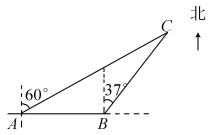
【题目】一艘观光游船从港口A处以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发生了求救信号,一艘在港口正东方向B处的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里/时的速度前往救援,求海警船到达事故船C处所需的大约时间.(参考数据:sin53°≈0.8,cos53°≈0.6)
参考答案:
【答案】1.25h
【解析】
试题分析:作CD⊥AB于点D,根据Rt△ACD的三角函数求出CD的长度,然后根据Rt△CBD的三角函数求出BC的长度,然后根据时间=路程÷速度得出答案.
试题解析:作CD⊥AB于点D,在Rt△ACD中,AC=80,∠CAB=30°, ∴CD=40(海里),
在Rt△CBD中,CB=![]() ≈
≈![]() =50(海里),∴航行的时间t=
=50(海里),∴航行的时间t=![]() =1.25(h)
=1.25(h)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列对数学符号|﹣2017|描述正确的是( )
A. 2017的相反数 B. ﹣2017的绝对值
C. ﹣2017的倒数 D. ﹣2017的相反数
-
科目: 来源: 题型:
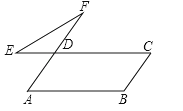
查看答案和解析>>【题目】如图,在平行四边形ABCD中,∠B=110°,延长AD至F,延长CD至E,连接EF,则∠E+∠F的值为度.
-
科目: 来源: 题型:
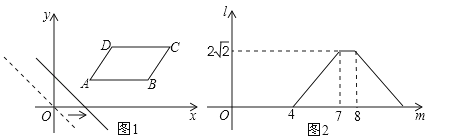
查看答案和解析>>【题目】如图1,在平面直角坐标系中,将ABCD放置在第一象限,且AB∥x轴.直线y=﹣x从原点出发沿x轴正方向平移,在平移过程中直线被平行四边形截得的线段长度l与直线在x轴上平移的距离m的函数图象如图2所示,那么AD的长为
-
科目: 来源: 题型:
查看答案和解析>>【题目】用配方法解关于x的一元二次方程x2﹣2x﹣3=0,配方后的方程可以是( )
A.(x﹣1)2=4
B.(x+1)2=4
C.(x﹣1)2=16
D.(x+1)2=16 -
科目: 来源: 题型:
查看答案和解析>>【题目】袋中装有除颜色外完全相同的2个红球和1个绿球.
(1)现从袋中摸出1个球后放回,混合均匀后再摸出1个球.请用画树状图或列表的方法,求第一次摸到绿球,第二次摸到红球的概率;
(2)先从袋中摸出1个球后不放回,再摸出1个球,则两次摸到的球中有1个绿球和1个红球的概率是多少?请直接写出结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程x2﹣9=0的解是 .
相关试题

