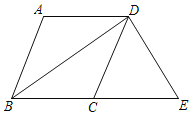
【题目】如图,面积为24的ABCD中,对角线BD平分∠ABC,过点D作DE⊥BD交BC的延长线于点E,DE=6,则sin∠DCE的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
参考答案:
【答案】A
【解析】
连接AC,过点D作DF⊥BE于点E,由BD平分∠ABC证得四边形ABCD是菱形,利用DE⊥BD得到OC∥ED求出AC,根据ABCD面积为24求出BD,再由勾股定理求出BC,设CF=x,则BF=5+x,利用BD2﹣BF2=DC2﹣CF2求出x得到DF,即可求出答案.
解:连接AC,过点D作DF⊥BE于点E,
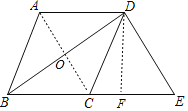
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∵![]() ABCD中,AD∥BC,
ABCD中,AD∥BC,
∴∠ADB=∠DBC,
∴∠ADB=∠ABD,
∴AB=BC,
∴四边形ABCD是菱形,
∴AC⊥BD,OB=OD,
∵DE⊥BD,
∴OC∥ED,
∵DE=6,
∴OC=![]() ,
,
∴AC=6,
∵![]() ABCD的面积为24,
ABCD的面积为24,
∴![]() ,
,
∴BD=8,
∴![]() =
=![]() =5,
=5,
设CF=x,则BF=5+x,
由BD2﹣BF2=DC2﹣CF2可得:82﹣(5+x)2=52﹣x2,
解得x=![]() ,
,
∴DF=![]() ,
,
∴sin∠DCE=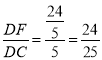 .
.
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中有两点
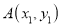 、
、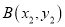 ,我们定义
,我们定义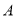 、
、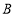 两点间的“
两点间的“ 值”直角距离为
值”直角距离为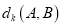 ,且满足
,且满足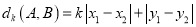 ,其中
,其中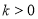 .小静和佳佳在解决问题:(求点
.小静和佳佳在解决问题:(求点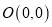 与点
与点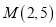 的“1值”直角距离
的“1值”直角距离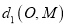 )时,采用了两种不同的方法:
)时,采用了两种不同的方法:(方法一):
 ;
;(方法二):如图1,过点
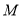 作
作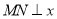 轴于点
轴于点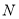 ,过点
,过点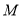 作直线
作直线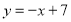 与
与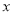 轴交于点
轴交于点 ,则
,则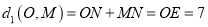
请你参照以上两种方法,解决下列问题:
(1)已知点
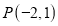 ,点
,点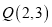 ,则
,则 、
、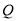 两点间的“2值”直角距离
两点间的“2值”直角距离 .
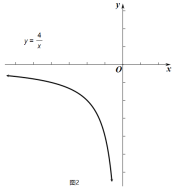
.(2)函数
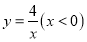 的图像如图2所示,点
的图像如图2所示,点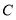 为其图像上一动点,满足
为其图像上一动点,满足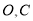 两点间的“
两点间的“ 值”直角距离
值”直角距离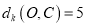 ,且符合条件的点
,且符合条件的点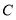 有且仅有一个,求出符合条件的“
有且仅有一个,求出符合条件的“ 值”和点
值”和点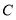 坐标.
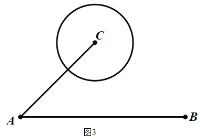
坐标.(3)城市的许多街道是相互垂直或平行的,因此,往往不能沿直线行走到达目的地,只能按直角拐弯的方式行走,因此,两地之间修建垂直和平行的街道常常转化为两点间的“
 值”直角距离,
值”直角距离,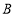 地位于
地位于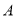 地的正东方向上,
地的正东方向上,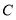 地在
地在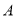 点东北方向上且相距
点东北方向上且相距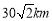 ,以
,以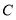 为圆心修建了一个半径为
为圆心修建了一个半径为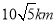 的圆形湿地公园,现在要在公园和
的圆形湿地公园,现在要在公园和 地之间修建观光步道.步道只能东西或者南北走向,并且东西方向每千米成本是20万元,南北方向每千米的成本是10万元,问:修建这一规光步道至少要多少万元?
地之间修建观光步道.步道只能东西或者南北走向,并且东西方向每千米成本是20万元,南北方向每千米的成本是10万元,问:修建这一规光步道至少要多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,热气球的探测器显示,从热气球A看一栋大楼顶部B的俯角为
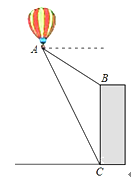 ,看这栋大楼底部C的俯角为
,看这栋大楼底部C的俯角为 ,热气球A的高度为270米,则这栋大楼的高度为______米
,热气球A的高度为270米,则这栋大楼的高度为______米

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,直线DE与⊙O相切于点C,过A,B分别作AD⊥DE,BE⊥DE,垂足为点D,E,连接AC,BC,若AD=
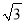 ,CE=3,则
,CE=3,则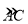 的长为( )
的长为( )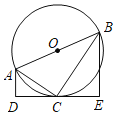
A.
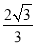 B.
B.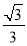 πC.
πC.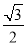 πD.
πD.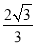 π
π -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(﹣3,y1),B(2,y2)均在抛物线y=ax2+bx+c上,点P(m,n)是该抛物线的顶点,若y1>y2≥n,则m的取值范围是( )
A.﹣3<m<2B.﹣
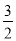 <m<-
<m<-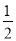 C.m>﹣
C.m>﹣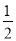 D.m>2
D.m>2 -
科目: 来源: 题型:
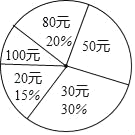
查看答案和解析>>【题目】在“全民读书月”活动中,小明调查了班级里40名同学本学期购买课外书的费用情况,并将结果绘制成如图所示的统计表和扇形统计图,请根据相关信息,解答下列问题:(直接填写结果)
费用(元)
20
30
50
80
100
人数
6
a
10
b
4
(1)本次调查获取的样本数据的众数是 元,中位数是 元;
(2)扇形统计图中,“50元”所对应的圆心角的度数为 度,该班学生购买课外书的平均费用为 元;
(3)若该校共有学生1000人,根据样本数据,估计本学期购买课外书花费50元的学生有 人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.
(1)求证:BG=CF;
(2)请你判断BE+CF与EF的大小关系,并说明理由.

相关试题

