【题目】工匠制作某种金属工具要进行材料煅烧和锻造两个工序,即需要将材料烧到800℃,然后停止煅烧进行锻造操作,经过8min时,材料温度降为600℃.煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时,温度y(℃)与时间x(min)成反比例函数关系(如图).已知该材料初始温度是32℃.
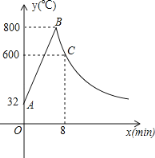
(1)分别求出材料煅烧和锻造时y与x的函数关系式,并且写出自变量x的取值范围;
(2)根据工艺要求,当材料温度低于480℃时,须停止操作.那么锻造的操作时间有多长?
参考答案:
【答案】(1)材料加热时,![]() 与
与![]() 的函数关系式为
的函数关系式为![]() ,停止加热进行锻造时
,停止加热进行锻造时![]() 与
与![]() 的函数关系式为:
的函数关系式为:![]() ;(2)锻造的操作时间有4分钟.
;(2)锻造的操作时间有4分钟.
【解析】
试题分析:(1)根据题意,材料煅烧时,温度![]() 与时间
与时间![]() 成一次函数关系,煅烧结束时,温度
成一次函数关系,煅烧结束时,温度![]() 与
与![]() 时间成反比例函数关系,将题中数据代入,用待定系数法可得两个函数的关系式;
时间成反比例函数关系,将题中数据代入,用待定系数法可得两个函数的关系式;
(2)把![]() 代入
代入![]() 中,求解得出答案即可.
中,求解得出答案即可.
试题解析:(1)停止加热时,设![]() ,由题意得
,由题意得![]() ,解得
,解得![]() ,当
,当![]() 时,
时,![]() 解得
解得![]() ,点B的坐标为(6,800);材料加热时,设
,点B的坐标为(6,800);材料加热时,设![]() ,由题意得
,由题意得![]() ,解得
,解得![]() .材料加热时,
.材料加热时,![]() 与
与![]() 的函数关系式为
的函数关系式为![]() ,停止加热进行锻造时
,停止加热进行锻造时![]() 与
与![]() 的函数关系式为:
的函数关系式为:![]() .
.
(2)把![]() 代入
代入![]() 中,得
中,得![]()
![]() 分钟.故锻造的操作时间为4分钟.
分钟.故锻造的操作时间为4分钟.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一种躺椅及其简化结构示意图,扶手AB与座板CD都平行于地面,靠背DM与支架OE平行,前支架OE与后支架OF分别与CD交于点G和点D,AB与DM交于点N,量得∠EOF=90°,∠ODC=30°,ON=40cm,EG=30cm.
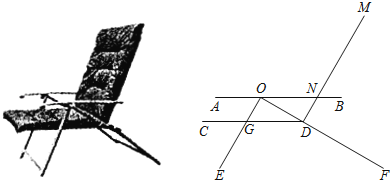
(1)求两支架落点E、F之间的距离;
(2)若MN=60cm,求躺椅的高度(点M到地面的距离,结果取整数).
(参考数据:sin60°=
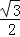 ,cos60°=
,cos60°= ,tan60°=
,tan60°=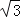 ≈1.73,可使用科学计算器)
≈1.73,可使用科学计算器) -
科目: 来源: 题型:
查看答案和解析>>【题目】直角三角形两边长为6和8,那么第三边的平方为____________。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知凸n边形的每一个外角均为45°,则n=__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若函数y=mx2+2x+1的图象与x轴只有一个公共点,则常数m的值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的周长为15cm,其中一边长为3cm.则该等腰三角形的腰长为 ( )
A. 3cm B. 6cm C. 3cm或6cm D. 3cm或9cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过y轴上任意一点P,作x轴的平行线,分别与反比例函数
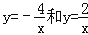 的图象交于A点和B点,若C为x轴上任意一点,连接AC,BC,则△ABC的面积为( )
的图象交于A点和B点,若C为x轴上任意一点,连接AC,BC,则△ABC的面积为( )
A.3 B.4 C.5 D.6
相关试题

