【题目】如图是一种躺椅及其简化结构示意图,扶手AB与座板CD都平行于地面,靠背DM与支架OE平行,前支架OE与后支架OF分别与CD交于点G和点D,AB与DM交于点N,量得∠EOF=90°,∠ODC=30°,ON=40cm,EG=30cm.
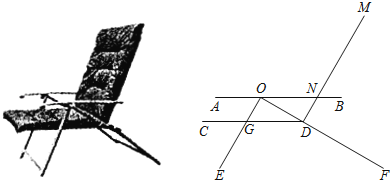
(1)求两支架落点E、F之间的距离;
(2)若MN=60cm,求躺椅的高度(点M到地面的距离,结果取整数).
(参考数据:sin60°=![]() ,cos60°=
,cos60°=![]() ,tan60°=
,tan60°=![]() ≈1.73,可使用科学计算器)
≈1.73,可使用科学计算器)
参考答案:
【答案】(1)EF=100cm.(2)95cm.
【解析】
试题分析:(1)利用平行线分线段成比例定理得出![]() ,利用平行四边形的判定与性质进而求出即可;
,利用平行四边形的判定与性质进而求出即可;
(2)利用四边形ONHE是平行四边形,进而得出NH=OE=50cm,∠MHF=∠E=60°,利用MP=110sin60°求出即可.
解:(1)连接EF.
∵CD平行于地面,
∴GD∥EF.
∴![]() .
.
又∵AB∥EF,
∴AB∥CD.
而OE∥DM,
则四边形OGDN是平行四边形.
∴OG=DN,GD=ON.
∵ON=40cm,∠EOF=90°,∠ODC=30°,
∴GD=40cm,OG=![]() GD=20cm,又EG=30cm,
GD=20cm,又EG=30cm,
即![]() ,得EF=100cm.
,得EF=100cm.
(2)延长MD交EF于点H,过点M作MP⊥EF于点P.
∵四边形ONHE是平行四边形,
∴NH=OE=50cm,∠MHF=∠E=60°.
由于MN=60cm,∴MH=110cm.
在Rt△MHP中,MP=MHsin∠MHP,
即MP=110sin60°=110×![]() =55
=55![]() ≈95(cm).
≈95(cm).
答:躺椅的高度约为95cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】商场销售某种冰箱,该种冰箱每台进价为2500元.已知原销售价为每台2900元时,平均每天能售出8台.若在原销售价的基础上每台降价50元,则平均每天可多售出4台.设每台冰箱的实际售价比原销售价降低了x元.
(1)填表(不需化简):
每天的销售量/台
每台销售利润/元
降价前
8
400
降价后
(2)商场为使这种冰箱平均每天的销售利润达到5000元,则每台冰箱的实际售价应定为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠C=90°,AC=8cm,BC=4cm.一动点P从点C出发沿着CB方向以1cm/s的速度运动,另一动点Q从A出发沿着AC方向以2cm/s的速度运动.P,Q两点同时出发,运动时间为t(s).

(1)若△PCQ的面积是△ABC面积的
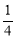 ,求t的值;
,求t的值;(2)△PCQ的面积能否为△ABC面积的一半?若能,求出t的值;若不能,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正三角形中心旋转 度的整倍数之后能和自己重合.
-
科目: 来源: 题型:
查看答案和解析>>【题目】直角三角形两边长为6和8,那么第三边的平方为____________。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知凸n边形的每一个外角均为45°,则n=__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】工匠制作某种金属工具要进行材料煅烧和锻造两个工序,即需要将材料烧到800℃,然后停止煅烧进行锻造操作,经过8min时,材料温度降为600℃.煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时,温度y(℃)与时间x(min)成反比例函数关系(如图).已知该材料初始温度是32℃.
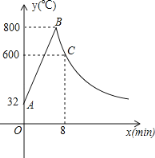
(1)分别求出材料煅烧和锻造时y与x的函数关系式,并且写出自变量x的取值范围;
(2)根据工艺要求,当材料温度低于480℃时,须停止操作.那么锻造的操作时间有多长?
相关试题

