【题目】我们知道,在等腰直角三角形和含有30°角的直角三角形中,三边之间的比例关系分别如图所示:
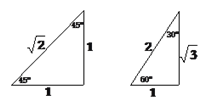
试借助上述结论,构造图形,解决下面的问题:
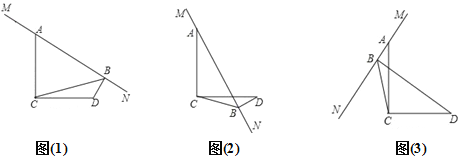
如图(1),已知∠ACD=90°,MN是过点A的直线,AC=DC,DB⊥MN于点B,
(1) 求证: BD+AB=![]() CB;
CB;
(2) 当MN绕A旋转到如图(2)和图(3)两个位置时,BD、AB、CB满足什么样关系式,请写出你的猜想,并对图(3)给予证明;
(3) MN在绕点A旋转过程中,当∠BCD=30°,BD=![]() 时,则CD= ,CB= .
时,则CD= ,CB= .
参考答案:
【答案】(1)证明见解析;(2) ![]() ;
; ![]() ;(3)2;
;(3)2; ![]() .
.
【解析】试题分析:(1)过点C作CE⊥CB于点C,与MN交于点E,证明△ACE≌△DCB,则△ECB为等腰直角三角形,据此即可得到BE=![]() CB,根据BE=AE+AB即可证得;
CB,根据BE=AE+AB即可证得;
(2)过点C作CE⊥CB于点C,与MN交于点E,证明△ACE≌△DCB,则△ECB为等腰直角三角形,据此即可得到BE=![]() CB,根据BE=AB-AE即可证得;
CB,根据BE=AB-AE即可证得;
(3)过点B作BH⊥CD于点H,证明△BDH是等腰直角三角形,求得DH的长,在直角△BCH中,利用直角三角形中30°的锐角所对的直角边等于斜边的一半,即可求得.
试题解析:(1)过点C作CE⊥CB于点C,与MN交于点E,
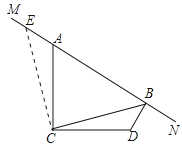
∵∠ACB+∠BCD=90°,∠ACB+∠ACE=90°,
∴∠BCD=∠ACE.
∵四边形ACDB内角和为360°,
∴∠BDC+∠CAB=180°.
∵∠EAC+∠CAB=180°,
∴∠EAC=∠BDC.
又∵AC=DC,
∴△ACE≌△DCB,
∴AE=DB,CE=CB,
∴△ECB为等腰直角三角形,
∴BE=![]() CB.
CB.
又∵BE=AE+AB,
∴BE=BD+AB,
∴BD+AB=![]() CB;
CB;
(2)如图(2) ABBD=![]() CB.理由如下:
CB.理由如下:

过点C作CE⊥CB于点C,与MN交于点E,
∵∠ACD=90°,
∴∠ACE=90°∠DCE,∠BCD=90°∠ECD,
∴∠BCD=∠ACE.
∵DB⊥MN,
∴∠CAE=90°∠AFC,∠D=90°∠BFD,
∵∠AFC=∠BFD,
∴∠CAE=∠D,
在△ACE和△DCB中, 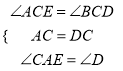 ,
,
∴△ACE≌△DCB(ASA),
∴AE=DB,CE=CB,
∴△ECB为等腰直角三角形,
∴BE=![]() CB.
CB.
又∵BE=ABAE,
∴BE=ABBD,
∴ABBD=![]() CB.
CB.
如图(3):BDAB=![]() CB.理由如下:
CB.理由如下:
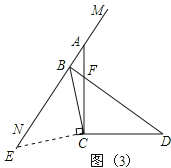
过点C作CE⊥CB于点C,与MN交于点E,
∵∠ACD=90°,
∴∠ACE=90°+∠ACB,∠BCD=90°+∠ACB,
∴∠BCD=∠ACE.
∵DB⊥MN,
∴∠CAE=90°∠AFB,∠D=90°∠CFD,
∵∠AFB=∠CFD,
∴∠CAE=∠D,
又∵AC=DC,
∴△ACE≌△DCB,
∴AE=DB,CE=CB,
∴△ECB为等腰直角三角形,
∴BE=![]() CB.
CB.
又∵BE=AEAB,
∴BE=BDAB,
∴BDAB=![]() CB.
CB.
(3)MN在绕点A旋转过程中,这个的意思并没有指明是哪种情况,
∴综合了第一个图和第二个图两种情况,
若是第1个图:
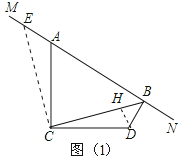
由(1)得:△ACE≌△DCB,CE=CB,
∴△ECB为等腰直角三角形,
∴∠AEC=45°=∠CBD,
过D作DH⊥CB.则△DHB为等腰直角三角形。
BD=![]() BH,
BH,
∴BH=DH=1.
直角△CDH中,∠DCH=30°,
∴CD=2DH=2,CH=![]() .
.
∴CB=![]() +1;
+1;
若是第二个图:过D作DH⊥CB交CB延长线于H.
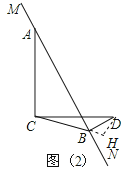
解法类似上面,CD=2,得出CB=![]() 1;
1;
故答案为:2, ![]() +1或
+1或![]() 1.
1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x2+2x﹣5=0,则x3+3x2﹣3x﹣5的值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的袋中装有除颜色外均相同的8个黑球、4个白球和若干个红球.每次摇匀后随机摸出一个球,记下颜色后再放回袋中,通过大量重复摸球试验后,发现摸到红球的频率稳定于0.4,由此可估计袋中约有红球个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一组数据10,8,9,a,5众数是8,求这组数据的中位数_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程
(1)5x﹣6=3x﹣4;
(2)3(x+2)=5x
-
科目: 来源: 题型:
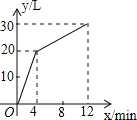
查看答案和解析>>【题目】一个有进水管和出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分钟的进水量和出水量是两个常数,容器内的水量y(L)与时间x(min)之间的关系如图所示,求:
(1) 出水管每分钟的出水量是多少(L);
(2) 第8分钟时,容器内的水量是多少(L).
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:(﹣2x2+6+3x)+(6x﹣3+3x2),其中x=﹣2.
相关试题

