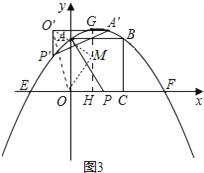
【题目】如图:已知正方形OABC的边OC、OA分别在x轴和y轴的正半轴上,点B坐标为(4,4).二次函数![]() 的图象经过点A、B,且与x轴的交点为E、F.点P在线段EF上运动,过点O作OH⊥AP于点H,直线OH交直线BC于点D,连接AD.
的图象经过点A、B,且与x轴的交点为E、F.点P在线段EF上运动,过点O作OH⊥AP于点H,直线OH交直线BC于点D,连接AD.
(1)求b、c的值;
(2)在点P运动过程中,当△AOP与以A、B、D为顶点的三角形相似时,求点P的坐标;
(3)在点P运动到OC中点时,能否将△AOP绕平面内某点旋转90°后使得△AOP的两个顶点落在x轴上方的抛物线上?若能,请直接写出旋转中心M的坐标;若不能,请说明理由.

参考答案:
【答案】(1)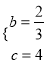 (2)P1(2,0);P2(2+2
(2)P1(2,0);P2(2+2![]() ,0);P3(2﹣2
,0);P3(2﹣2![]() ,0).(3)(2,2),(1
,0).(3)(2,2),(1![]() ,3
,3![]() ),(﹣
),(﹣![]() ,
, ![]() );
);
【解析】(1)把(0,4),(4,4)分别代入y=﹣![]() x2+bx+c中,
x2+bx+c中,
得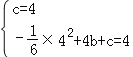 ,
,
解得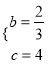 ;
;
(2)解:设P(t,0)①当P点在线段OC上时,如原图所示;
∵∠OAP<45°,∠BAD<45°
∵若△AOP∽△ABD,AO=AB,
∴OP=BD,
∴OP=BD=CD=2,
∴t=2
∴P1(2,0).
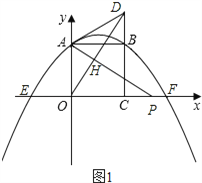
②点P在线段CF上时,如图1所示:
∵∠ADB>∠ODC,
∵∠APO=∠ODC,
∴∠ABD>∠APO,
∴若△AOP∽△ABD,则![]() =
=![]() ,
,
在△AOP与△OCD中
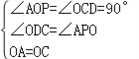
∴△AOP≌△OCD(AAS),
∴OP=CD,
∴DB=PC=t﹣4,
∴![]() ,
,
解得t=2﹣2![]() (舍去)或t=2+2
(舍去)或t=2+2![]() ,
,
∴P2(2+2![]() ,0).
,0).

③点P在线段OE上时,如图2所示;
∵∠COD+∠ODC=90°,∠HOP+∠APO=90°,∠COD=∠HOP,
∴∠ODC=∠APO,
∵∠ODC>∠ADB,
∴∠APO>∠ADB,
∴若△AOP∽△ABD,则![]() =
=![]() ,
,
在△AOP与△OCD中
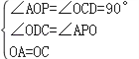
∴△AOP≌△OCD(AAS),
∴OP=CD,
∴DB=PC=4﹣t,
∴![]() ,
,
解得t=2+2![]() (舍去)或t=2﹣2
(舍去)或t=2﹣2![]() ,
,
∴P3(2﹣2![]() ,0).
,0).
(3)(2,2),(1![]() ,3
,3![]() ),(﹣
),(﹣![]() ,
, ![]() );
);
如图3所示:设△AOP绕点M顺时针旋转90°得到△A′O′P′,且P′、A′两点在抛物线y=﹣![]() x2+
x2+![]() x+4上,
x+4上,
设O′(x,y),则P′(x,y﹣2),A′(x+4,y)
∴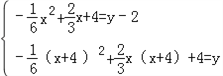 ,
,
解得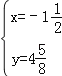 ,
,
作MG⊥O′A′于G,MH⊥OC于H,设M(a,b),
∵△O′MG≌△MOH,
∴O′G=MH=b,MG=OH=a,
∴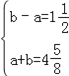 ,
,
解得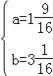 ,
,
∴M(1![]() ,3
,3![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知:如图1,等腰直角三角形ABC中,∠B=90°,AD是∠BAC的外角平分线,交CB边的延长线于点D.

求证:BD=AB+AC.
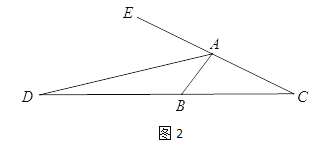
(2)对于任意三角形ABC,∠ABC=2∠C,AD是∠BAC的外角平分线,交CB边的延长线于点D,如图2,请你写出线段AC、AB、BD之间的数量关系并加以证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组数据分别为三角形的三边长,不能组成直角三角形的是( )
A. 9,12,15 B. 7,24,25 C. 6,8,10 D. 3,5,7
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小华和小丽两人玩游戏,她们准备了A、B两个分别被平均分成三个、四个扇形的转盘.游戏规则:小华转动A盘、小丽转动B盘.转动过程中,指针保持不动,如果指针恰好指在分割线上,则重转一次,直到指针指向一个数字所在的区域为止.两个转盘停止后指针所指区域内的数字之和小于6,小华获胜.指针所指区域内的数字之和大于6,小丽获胜.
(1)用树状图或列表法求小华、小丽获胜的概率;
(2)这个游戏规则对双方公平吗?请判断并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】把(+5)﹣(+3)﹣(﹣1)+(﹣4)写成省略括号的和的形式是( )
A.﹣5﹣3+1﹣4
B.5﹣3﹣1﹣4
C.5﹣3+1﹣4
D.5+3+1﹣4 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算结果中等于3的数是( )
A.|﹣7|+|+4|
B.|(﹣7)+(+4)|
C.|+7|+|﹣4|
D.|(﹣7)﹣(﹣3)| -
科目: 来源: 题型:
查看答案和解析>>【题目】证明:在一个三角形中,至少有一个内角小于或等于60度.
相关试题

