Question

【题目】（1）已知：如图1，等腰直角三角形ABC中，∠B=90°，AD是∠BAC的外角平分线，交CB边的延长线于点D．

求证：BD=AB+AC．

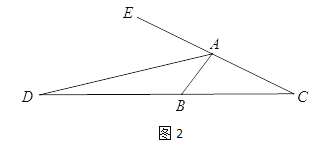
（2）对于任意三角形ABC，∠ABC=2∠C，AD是∠BAC的外角平分线，交CB边的延长线于点D，如图2，请你写出线段AC、AB、BD之间的数量关系并加以证明．

Answer 1

【答案】（1）答案见解析；（2）DB=AB+AC．

【解析】试题分析：（1）如图，在AE上截取AF=AB，连接DF，先证明△ABD≌△AFD，可得DF=DB，∠DBA=∠DFA=90°，再利用等腰直角三角形的性质证得DF=FC，即可证得结论；（2）BD=AB+AC，如图，在AE上截取AF=AB，连接DF，先证明△ABD≌△AFD，可得DF=DB，∠DBA=∠DFA，，再利用三角形外角的性质和已知条件证得∠C=∠FDC，根据等腰三角形的性质可得DF=FC，即可证得结论.

试题解析：

（1）如图，在AE上截取AF=AB，连接DF.

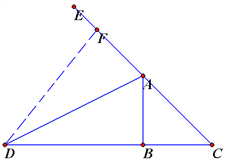
∵AD是∠BAC的外角平分线，

∴∠BAD=∠DAE.

在△ABD和△AFD中，

,

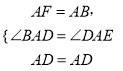∴△ABD≌△AFD，

∴DF=DB，∠DBA=∠DFA=90°，

∵△ABC为等腰直角三角形，

∴∠C=45°，

∴△FDC为等腰直角三角形，

∴DF=FC.

∴BD=FC=AF+AC=AB+AC.

（2）BD=AB+AC，理由如下：

如图，在AE上截取AF=AB，连接DF.

∵AD是∠BAC的外角平分线，

∴∠BAD=∠DAE.

在△ABD和△AFD中，

,

∴△ABD≌△AFD，

∴DF=DB，∠DBA=∠DFA，

∴∠EFD=∠ABC，

∵∠ABC=2∠C，∠ABC=∠C+∠FDC，

∴∠C=∠FDC，

∴DF=FC.

∴BD=FC=AF+AC=AB+AC.