【题目】如图,直线y=﹣x+3与x轴、y轴分别交于点B、点C,经过B、C两点的抛物线y=x2+bx+c与x轴的另一个交点为A,顶点为P.
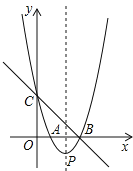
(1)求该抛物线的解析式;
(2)连接AC,在x轴上是否存在点Q,使以P、B、Q为顶点的三角形与△ABC相似?若存在,请求出点Q的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)抛物线解析式为y=x2﹣4x+3;(2)Q点的坐标为(0,0)或(![]() ,0).
,0).
【解析】
试题分析:(1)先确定出点B,C坐标,再用待定系数法求函数解析式;
(2)先求出BA=2,BC=3![]() ,BP=
,BP=![]() ,然后分两种情况①由△ABC∽△PBQ,得到
,然后分两种情况①由△ABC∽△PBQ,得到![]() ,求出BQ,②由△ABC∽△QBP得
,求出BQ,②由△ABC∽△QBP得![]() ,求出BQ,即可.
,求出BQ,即可.
解:(1)∵直线y=﹣x+3与x轴、y轴分别交于点B、点C,
令x=0,得y=3,
∴C(0,3),
令y=0,得x=3,
∴B(3,0),
∵经过B、C两点的抛物线y=x2+bx+c
∴![]() ,
,
解得![]() ,
,
∴抛物线解析式为y=x2﹣4x+3;
(2)由(1),得A(1,0),连接BP,
∵∠CBA=∠ABP=45°,
∵抛物线解析式为y=x2﹣4x+3;
∴P(2,﹣1),
∵A(1,0),B(3,0),C(0,3),
∴BA=2,BC=3![]() ,BP=
,BP=![]() ,
,
当△ABC∽△PBQ时,
∴![]() ,
,
∴![]() ,
,
∴BQ=3,
∴Q(0,0),
当△ABC∽△QBP时,
∴![]() ,
,
∴![]() ,
,
∴BQ=![]() ,
,
∴Q(![]() ,0),
,0),
∴Q点的坐标为(0,0)或(![]() ,0).
,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转,这三种可能性大小相同,现在两辆汽车经过这个十字路口.
(1)请用“树形图”或“列表法”列举出这两辆汽车行驶方向所有可能的结果;
(2)求这两辆汽车都向左转的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的一边长等于5,一边长等于10,求它的周长。
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.形状相同的两个三角形全等
B.面积相等的两个三角形全等
C.完全重合的两个三角形全等
D.所有的等边三角形全等
-
科目: 来源: 题型:
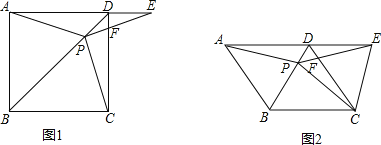
查看答案和解析>>【题目】如图1在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120度时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】比较大小:﹣30__﹣40(用“>”“=”或“<”表示).
-
科目: 来源: 题型:
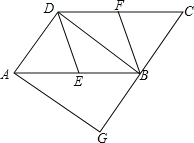
查看答案和解析>>【题目】如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,过A点作AG∥DB,交CB的延长线于点G.
(1)求证:DE∥BF;
(2)若∠G=90,求证:四边形DEBF是菱形.
相关试题

