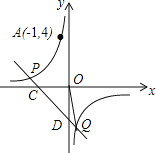
【题目】如图,反比例函数y=![]() 的图象经过点(-2,2),直线y=-x+b(b≠0)与双曲线y=
的图象经过点(-2,2),直线y=-x+b(b≠0)与双曲线y=![]() 在第二、四象限分别相交于P,Q两点,与x轴、y轴分别相交于A,B两点.
在第二、四象限分别相交于P,Q两点,与x轴、y轴分别相交于A,B两点.
(1)求k的值;
(2)当b=-2时,求△OAB的面积,并求出交点P的坐标;
(3)连接OQ,是否存在实数b使S△OBQ=S△OAB?若存在,请求出b的值;若不存在,请说明理由.

参考答案:
【答案】(1)-4;(2) (-![]() -1,
-1, ![]() -1) ;(3)存在.
-1) ;(3)存在.
【解析】试题分析:(1)根据反比例函数的图象上点的坐标特征易得k=-4;
(2)当b=-2时,直线解析式为y=-x-2,则利用坐标轴上点的坐标特征可求出C(-2,0),D(0,-2),然后根据三角形面积公式求解;
(3)先表示出C(b,0),根据三角形面积公式,由于S△ODQ=S△OCD,所以点Q和点C到OD的距离相等,则Q的横坐标为(-b,0),利用直线解析式可得到Q(-b,2b),再根据反比例函数的图象上点的坐标特征得到-b2b=-4,然后解方程即可得到满足条件的b的值.
试题解析:(1)∵反比例函数y=![]() 的图象经过点A(-1,4),
的图象经过点A(-1,4),
∴k=-1×4=-4;
(2)当b=-2时,直线解析式为y=-x-2,
∵y=0时,-x-2=0,解得x=-2,
∴C(-2,0),
∵当x=0时,y=-x-2=-2,
∴D(0,-2),
∴S△OCD=![]() ×2×2=2;
×2×2=2;
(3)存在.
当y=0时,-x+b=0,解得x=b,则C(b,0),
∵S△ODQ=S△OCD,
∴点Q和点C到OD的距离相等,
而Q点在第四象限,
∴Q的横坐标为-b,
当x=-b时,y=-x+b=2b,则Q(-b,2b),
∵点Q在反比例函数y=-![]() 的图象上,
的图象上,
∴-b2b=-4,解得b=-![]() 或b=
或b=![]() (舍去),
(舍去),
∴b的值为-![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】圆锥形烟囱帽的底面直径为80cm,母线长为50cm,则这样的烟囱帽的侧面积是等于cm2 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中正确的是( )
A. 同位角相等
B. 如果一个等腰三角形的两边长分别为3和6,那么该三角形的周长为12或15
C. 直线外一点与直线上各点连接的所有线段中,垂线段最短
D. 事件“打开电视机,正好播放足球比赛”是必然事件
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果+3吨表示运入仓库的大米吨数,那么运出5吨大米表示为:( )
A.-5吨
B.+5吨
C.-3吨
D.+3吨 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A1,A2,A3,…,An是x轴上的点,且OA1=A1A2=A2A3=…=An-1An=1,分别过点A1,A2,A3,…,An作x轴的垂线交反比例函数y=
 (x>0)的图象于点B1,B2,B3,…,Bn,过点B2作B2P1⊥A1B1于点P1,过点B3作B3P2⊥A2B2于点P2……过点Bn+1作Bn+1Pn⊥AnBn于点Pn,记△B1P1B2的面积为S1,△B2P2B3的面积为S2……△BnPnBn+1的面积为Sn.求:
(x>0)的图象于点B1,B2,B3,…,Bn,过点B2作B2P1⊥A1B1于点P1,过点B3作B3P2⊥A2B2于点P2……过点Bn+1作Bn+1Pn⊥AnBn于点Pn,记△B1P1B2的面积为S1,△B2P2B3的面积为S2……△BnPnBn+1的面积为Sn.求:(1)S1=________;
(2)S10=________;
(3)S1+S2+S3+…+Sn的和.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正比例函数y=2x的图象过点(x1 , y1)、(x2 , y2).若x2﹣x1=1,则y2﹣y1= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A. a2+a3=a5B. a6÷a3=a3C. a2a3=a6D. (a3)2=a9
相关试题

