【题目】如图,在Rt△ABC中,∠C=90°,BD是角平分线,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E.
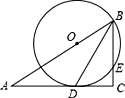
(1)求证:AC是⊙O的切线;
(2)若OB=5,CD=4,求BE的长.
参考答案:
【答案】(1)见解析 (2)6
【解析】分析:(1)连接OD,由BD为角平分线得到一对角相等,根据OB=OD,等边对等角得到一对角相等,等量代换得到一对内错角相等,进而确定出OD与BC平行,利用两直线平行同位角相等得到∠ODC为直角,即可得证;
(2)过O作OM垂直于BE,可得出四边形ODCM为矩形,在直角三角形OBM中,利用勾股定理求出BM的长,由垂径定理可得BE=2BM.
详解:(1)连接OD.
∵OD=OB,∴ ∠OBD=∠ODB.
∵BD是∠ABC的角平分线,∴ ∠OBD=∠CBD.
∵ ∠CBD=∠ODB,∴OD∥BC.
∵∠C=90,∴∠ODC=90,∴ OD⊥AC.
∵点D在⊙O上,
∴ AC是⊙O的切线.
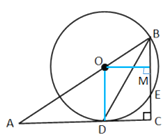
(2)过圆心O作OM![]() BC交BC于M.
BC交BC于M.
∵BE为⊙O 的弦,且OM![]() BE,∴BM=EM,
BE,∴BM=EM,
∵∠ODC=∠C=∠OMC= 90° ,
∴四边形ODCM为矩形,则OM=DC=4.
∵ OB=5,∴BM=![]() =3=EM,
=3=EM,
∴BE=BM+EM=6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2﹣2(k﹣1)x+k2=0有两个实数根x1,x2.
(1)求k的取值范围;
(2)若|x1+x2|=x1x2﹣1,求k的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=(3-k)x-2k2+18.
(1)k为何值时,它的图象经过原点?
(2)k为何值时,图象经过点(0,-2)?
(3)k为何值时,y随x的增大而减小?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(探索新知)
如图1,点
 在线段
在线段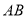 上,图中共有3条线段:
上,图中共有3条线段: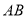 、
、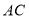 和
和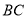 ,若其中有一条线段的长度是另一条线段长度的两倍,则称点
,若其中有一条线段的长度是另一条线段长度的两倍,则称点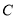 是线段
是线段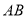 的“二倍点”.
的“二倍点”.(1)①一条线段的中点 这条线段的“二倍点”;(填“是”或“不是”)
②若线段
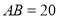 ,
,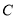 是线段
是线段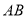 的“二倍点”,则
的“二倍点”,则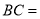 (写出所有结果)
(写出所有结果)(深入研究)
如图2,若线段
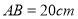 ,点
,点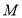 从点
从点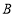 的位置开始,以每秒2
的位置开始,以每秒2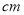 的速度向点
的速度向点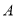 运动,当点
运动,当点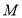 到达点
到达点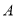 时停止运动,运动的时间为
时停止运动,运动的时间为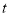 秒.
秒.(2)问
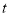 为何值时,点
为何值时,点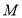 是线段
是线段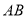 的“二倍点”;
的“二倍点”;(3)同时点
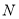 从点
从点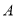 的位置开始,以每秒1
的位置开始,以每秒1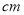 的速度向点
的速度向点 运动,并与点
运动,并与点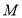 同时停止.请直接写出点
同时停止.请直接写出点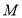 是线段
是线段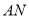 的“二倍点”时
的“二倍点”时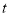 的值.
的值.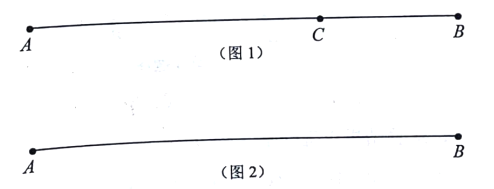
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解学生的安全意识情况,在全校范围内随机抽取部分学生进行问卷调查,根据调查结果,把学生的安全意识分成“淡薄”、“一般”、“较强”、“很强”四个层次,并绘制成如下两幅尚不完整的统计图.

根据以上信息,解答下列问题:
(1)这次调查一共抽取了 名学生,其中安全意识为“很强”的学生占被调查学生总数的百分比是 ;
(2)请将条形统计图补充完整;
(3)该校有1800名学生,现要对安全意识为“淡薄”、“一般”的学生强化安全教育,根据调查结果,估计全校需要强化安全教育的学生约有 名.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在矩形纸片ABCD中,AB=3cm,AD=5cm,折叠纸片使B点落在边AD上的E处,折痕为PQ,过点E作EF∥AB交PQ于F,连接BF.
(1)求证:四边形BFEP为菱形;
(2)当点E在AD边上移动时,折痕的端点P、Q也随之移动;
①当点Q与点C重合时(如图2),求菱形BFEP的边长;
②若限定P、Q分别在边BA、BC上移动,求出点E在边AD上移动的最大距离.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校计划在总费用
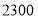 元的限额内,租用汽车送
元的限额内,租用汽车送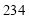 名学生和
名学生和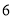 名教师集体参加校外实践活动,为确保安全,每辆汽车上至少要有
名教师集体参加校外实践活动,为确保安全,每辆汽车上至少要有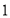 名教师.现有甲、乙两种大客车,它们的载客量和租金如下表所示.
名教师.现有甲、乙两种大客车,它们的载客量和租金如下表所示.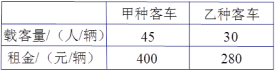
(1)根据题干所提供的信息,确定共需租用多少辆汽车?
(2)请你给学校选择一种最节省费用的租车方案.
相关试题

