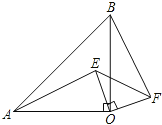
【题目】如图,已知,等腰Rt△OAB中,∠AOB=90o,等腰Rt△EOF中,∠EOF=90o,连结AE、BF.则AE与BF是什么关系?请说明理由.
参考答案:
【答案】相等和垂直
【解析】试题分析:①可以把要证明相等的线段AE,CF放到△AEO,△BFO中考虑全等的条件,由两个等腰直角三角形得AO=BO,OE=OF,再找夹角相等,这两个夹角都是直角减去∠BOE的结果,当然相等了,由此可以证明△AEO≌△BFO;
②由①知:∠OAC=∠OBF,∴∠BDA=∠AOB=90°,由此可以证明AE⊥BF.
试题解析:
①证明:在△AEO与△BFO中,
∵Rt△OAB与Rt△EOF等腰直角三角形,
∴AO=OB,OE=OF,∠AOE=90o-∠BOE=∠BOF,
∴△AEO≌△BFO,
∴AE=BF;
②延长AE交BF于D,交OB于C,则∠BCD=∠ACO,
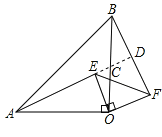
由①知:∠OAC=∠OBF,
∴∠BDA=∠AOB=90o,
∴AE⊥BF.
综合上述可得:AE与BF相等和垂直.
-
科目: 来源: 题型:
查看答案和解析>>【题目】旋转作图的步骤和方法:
(1)确定旋转中心,及;
(2)作出图形关键点经过旋转后的;
(3)按一定的顺序连接 -
科目: 来源: 题型:
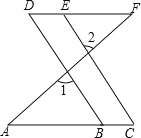
查看答案和解析>>【题目】如图,从①∠1=∠2 ②∠C=∠D ③∠A=∠F 三个条件中选出两个作为已知条件,另一个作为结论所组成的命题中,正确命题的个数为( )
A.0 B.1 C.2 D.3
-
科目: 来源: 题型:
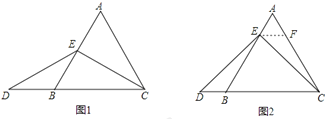
查看答案和解析>>【题目】数学课上,李老师出示了如下框中的题目.

小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况探索结论
当点E为AB的中点时,如图1,确定线段AE与的DB大小关系.请你直接写出结论:AE__________DB(填“>”,“<”或“=”).
(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AE__________DB(填“>”,“<”或“=”).理由如下:
如图2,过点E作EF∥BC,交AC于点F,(请你完成以下解答过程)
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,求CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:x2﹣16= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程ax2+x+a2﹣2a=0的一个根是x=0,则系数a=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC的两边长分别是3和5,则第三边x的取值范围是 .
相关试题

