【题目】(满分10分)如图,直径为AB的⊙O交![]() 的两条直角边BC、CD于点E、F,且
的两条直角边BC、CD于点E、F,且![]() ,连接BF.
,连接BF.
(1)求证CD为⊙O的切线;(2)当CF=1且∠D=30°时,求AD长.

参考答案:
【答案】(1) 证明见解析;(2) ![]() .
.
【解析】试题分析:(1)连接OF,只要证明OF∥BC,即可推出OF⊥CD,由此即可解决问题.
(2)连接AF.思想在Rt△BCF中,求出BC,再在Rt△DBC中,求出DB,在Rt△ABF中,求出AB,根据AD=DB-AB即可解决问题.
试题解析:
(1)连接OF.
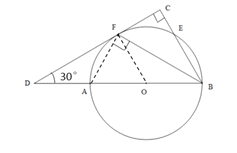
∵AF=EF ,∴∠CBF=∠FBA.
∵OF=OB,∴∠FBO=∠OFB .
∵点A、O、B三点共线,
∴∠CBF=∠OFB.
∴BC∥OF,∴∠OFC+∠C=180°.
∵∠C=90°,∴∠OFC=90°,即OF⊥DC.
∴CD为⊙O的切线.
(2) ∵∠D=30°,∴∠CBD=60°
∵AF=EF,∴∠CBF=∠DBF=![]() ∠CBD=30°
∠CBD=30°
在![]() , ∵FC=1,∠CBF=30°,∴BF=2CF=2.
, ∵FC=1,∠CBF=30°,∴BF=2CF=2.
∴![]()
连接AF.
∵AB是⊙O的直径,∴∠AFB=90°
在![]() ,∵∠ABF=30°,BF=2,∴AF=
,∵∠ABF=30°,BF=2,∴AF=![]() AB.
AB.
∴AB2=(![]() AB)2+BF2,即
AB)2+BF2,即![]() AB2=4,
AB2=4, ![]()
在![]() ,∵∠D=30°,BC=
,∵∠D=30°,BC=![]() ,∴BD=2BC=
,∴BD=2BC=![]() .
.
∴AD=DB-AB=2![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a﹣b=1,a2+ b2=25,则a+b的值为( )
A.7B.﹣7C.±7D.±9
-
科目: 来源: 题型:
查看答案和解析>>【题目】(满分8分)在北海市创建全国文明城活动中,需要20名志愿者担任“讲文明树新风”公益广告宣传工作,其中男生8人,女生12人.
(1)若从这20人中随机选取一人作为“展板挂图”讲解员,求选到女生的概率;
(2)若“广告策划”只在甲、乙两人中选一人,他们准备以游戏的方式决定由谁担任,游戏规则如下:将四张牌面数字分别为2,3,4,5的扑克牌洗匀后,数字朝下放于桌面,从中任取2张,若牌面数字之和为偶数,则甲担任,否则乙担任.试问这个游戏公平吗?请用树状图或列表法说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(满分6分)如图,在平面直角坐标系中,已知点B(4,2),BA⊥
 轴于A.
轴于A. (1)画出将△OAB绕原点旋转180°后所得的△OA1B1 ,并写出点B1 的坐标;
(2)将△OAB平移得到△O2A2B2,点A的对应点是A2(2,-4),点B的对应点B2
在坐标系中画出△O2A2B2 ;并写出B2的坐标;
(3)△OA1B1与△O2A2B2成中心对称吗?若是, 请直接写出对称中心点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列二次函数中,其图象对称轴为x=﹣2的是( )
A.y=(x+2)2
B.y=2x2﹣2
C.y=﹣2x2﹣2
D.y=2(x﹣2)2 -
科目: 来源: 题型:
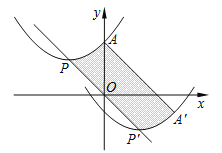
查看答案和解析>>【题目】如图,抛物线的顶点为P(﹣2,2),与y轴交于点A(0,3).若平移该抛物线使其顶点P沿直线移动到点P′(2,﹣2),点A的对应点为A′,则抛物线上PA段扫过的区域(阴影部分)的面积为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】等边三角形的对称轴有( )条.
A.1
B.2
C.3
D.4
相关试题

