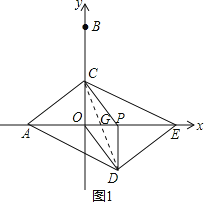
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(﹣3,0),(0,6).动点P从点O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点C从B出发,沿射线BO方向以每秒2个单位的速度运动,以CP,CO为邻边构造平行四边形PCOD,在线段OP延长线上取点E,使PE=AO,设点P运动的时间为t秒.

(1)直接写出当点C运动到线段OB的中点时,求t的值及点E的坐标.
(2)当点C在线段OB上运动时,四边形ADEC的面积为S.
①求证:四边形ADEC为平行四边形.
②写出s与t的函数关系式,并求出t的取值范围.
(3)是否存在某一时刻,使OC是PC的一半?若存在,求出t的值,若不存在,请说明理由.
参考答案:
【答案】(1)t=![]() ,E(
,E(![]() ,0);(2)①证明见解析;②s=36﹣6t﹣2t2( 0<t<3 );(3)存在,
,0);(2)①证明见解析;②s=36﹣6t﹣2t2( 0<t<3 );(3)存在,![]() ,或
,或![]() .
.
【解析】
(1)根据B的坐标(0,6)可得OB=6,再由BC=![]() OB,即可得BC=3,从而求出时间t,根据OE=OP+PE求出点E的坐标;
OB,即可得BC=3,从而求出时间t,根据OE=OP+PE求出点E的坐标;
(2)①连接CD交OP于点G,根据平行四边形的对角线互相平分的性质可得CG=DG,OG=PG,又因PE=AO,可得AG=EG,再根据对角线互相平分的四边形是平行四边形即可得四边形ADEC为平行四边形.;
②根据平行四边形的性质可得![]() ,用t表示出AE、OC的长,代入即可得s与t的函数关系式,再根据点C移动的距离和速度求出t的取值范围;
,用t表示出AE、OC的长,代入即可得s与t的函数关系式,再根据点C移动的距离和速度求出t的取值范围;
(3)在Rt△COP中,由已知OC是PC的一半,即可得∠CPO=30°,分两种情况,①点C在线段OB上,②点C在线段OB延长线上,在Rt△COP中,利用![]() 求解即可.
求解即可.
解:(1)∵B(0,6),∴OB=6,
点C运动到线段OB的中点时,BC=3,∴t=![]() ,
,
则OP=![]() ,OE=OP+PE=OP+OA=
,OE=OP+PE=OP+OA=![]() ,
,
∴E(![]() ,0);
,0);
(2)①如图1,连接CD交OP于点G,
在平行四边形PCOD中,CG=DG,OG=PG,
∵AO=PE,
∴AG=EG,
∴四边形ADEC是平行四边形;
②∵AE=t+6,OC=6﹣2t,
∴s=![]() ×AE×OC×2=(t+6)×(6﹣2t)
×AE×OC×2=(t+6)×(6﹣2t)
=36﹣6t﹣2t2( 0<t<3 )
(3)如图2,当点C在线段OB上时,OC=![]() PC,则∠CPO=30°,
PC,则∠CPO=30°,
![]() ,
,
即![]() ,解得,
,解得,![]() ,
,
如图3,当点C在线段OB延长线上时,
![]() ,解得,
,解得,![]() .
.


-
科目: 来源: 题型:
查看答案和解析>>【题目】为迎接全国文明城市的评选,市政府决定对春风路进行市政化改造,经过市场招标,决定聘请甲、乙两个工程队合作施工,已知春风路全长24千米,甲工程队每天施工的长度比乙工程队每天施工长度的多施工0.4千米,由甲工程队单独施工完成任务所需要的天数是乙工程队单独完成任务所需天数的
 .
.(1)求甲、乙两个工程队每天各施工多少千米?
(2)若甲工程队每天的施工费用为0.8万元,乙工程队每天的施工费用为0.5万元,要使两个工程队施工的总费用不超过7万元,则甲工程队至多施工多少天?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,AE、DE分别平分∠BAD、∠ADC,E点在BC上.

(1)求证:BC=2AB;
(2)若AB=3cm,∠B=60°,一动点F以1cm/s的速度从A点出发,沿线段AD运动,CF交DE于G,当CF∥AE时:
①求点F的运动时间t的值;②求线段AG的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1) (1-1
 -
- +
+ )×(-24)
)×(-24) (2) 1
 ×
× -(-
-(- )×2
)×2 +(-
+(- )+
)+
(3)(-119
 )×5
)×5 (4)(
 )÷(
)÷( )2÷|-
)2÷|- |+(-1)4+(0.25)2003×42003
|+(-1)4+(0.25)2003×42003 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图在数轴上A点表示数
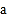 ,B点表示数
,B点表示数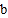 ,
,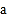 、
、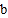 满足|
满足|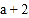 |+|
|+|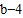 |=0;
|=0;
(1)点A表示的数为_____;点B表示的数为_____;
(2)若在原点O处放一挡板,一小球甲从点A处以1个单位/秒的速度向左运动;同时另一小球乙从点B处以2个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为t(秒),
①当t=1时,甲小球到原点的距离=_____;乙小球到原点的距离=_____.
当t=3时,甲小球到原点的距离=_____;乙小球到原点的距离=_____.
②试探究:甲,乙两小球到原点的距离可能相等吗?若不能,请说明理由.若能,请直接写出甲,乙两小球到原点的距离相等时经历的时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列函数中图象不经过第三象限的是( )
A.y=﹣3x﹣2B.y=
 C.y=﹣
C.y=﹣ x+1D.y=3x+2
x+1D.y=3x+2 -
科目: 来源: 题型:
查看答案和解析>>【题目】在平行四边形ABCD中,AB=10,∠ABC=60°,以AB为直径作⊙O,边CD切⊙O于点E.

(1)圆心O到CD的距离是______;
(2)求由弧AE、线段AD、DE所围成的阴影部分的面积.(结果保留π和根号)
相关试题

