【题目】为迎接全国文明城市的评选,市政府决定对春风路进行市政化改造,经过市场招标,决定聘请甲、乙两个工程队合作施工,已知春风路全长24千米,甲工程队每天施工的长度比乙工程队每天施工长度的多施工0.4千米,由甲工程队单独施工完成任务所需要的天数是乙工程队单独完成任务所需天数的![]() .
.
(1)求甲、乙两个工程队每天各施工多少千米?
(2)若甲工程队每天的施工费用为0.8万元,乙工程队每天的施工费用为0.5万元,要使两个工程队施工的总费用不超过7万元,则甲工程队至多施工多少天?
参考答案:
【答案】(1)甲队每天修2.4千米,乙队每天修2千米;(2)甲工程队至多施工5天.
【解析】
(1)设甲队每天完成x千米,则乙队每天完成(x﹣0.4)千米,然后依据甲工程队单独施工完成任务所需要的天数是乙工程队单独完成任务所需天数的![]() 列方程求解即可;
列方程求解即可;
(2)设甲队改造a米,则乙队改造(24﹣a)米,然后依据两个工程队施工的总费用不超过7万元列不等式求得a的范围,从而可求得甲工程队至多施工的天数.
(1)设甲队每天完成x千米,则乙队每天完成(x﹣0.4)千米.根据题意得:
![]() =
=![]() ×
×![]() ,
,
解得:x=2.4.
经检验,x=2.4是原方程的解.
2.4﹣0.4=2.
答:甲队每天修2.4千米,乙队每天修2千米.
(2)设甲队改造a米,则乙队改造(24﹣a)米.根据题意得:
![]() ×0.8+
×0.8+![]() ×0.5≤7,
×0.5≤7,
解得:a≤12.
![]() =5.
=5.
答:甲工程队至多施工5天.
-
科目: 来源: 题型:
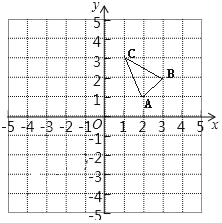
查看答案和解析>>【题目】在边长为1个单位长度的正方形网格中建立如图所示的平面直角坐标系,△ABC的顶点都在格点上,请解答下列问题:
(1)作出△ABC向左平移4个单位长度后得到的△A1B1C1,并写出点C1的坐标;
(2)将△A1B1C1绕原点O逆时针旋转90°得到△A2B2C2,请画出旋转后的△A2B2C2,并写出点C2的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过反比例函数y=
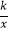 (x>0)的图像上一点A作AB⊥x轴于点B,连接AO,若S△AOB=2,则k的值为( )
(x>0)的图像上一点A作AB⊥x轴于点B,连接AO,若S△AOB=2,则k的值为( ) 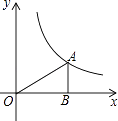
A.2
B.3
C.4
D.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AC是平行四边形ABCD的对角线,E、H分别为边BA和边BC延长线上的点,连接EH交AD、CD于点F、G,且EH∥AC.
(1)求证:EG=FH;
(2)若△ACD是等腰直角三角形,∠ACD=90°,F是AD的中点,AD=6,连接BF,求BF的长.

-
科目: 来源: 题型:
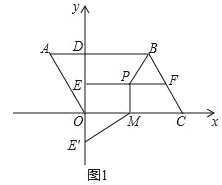
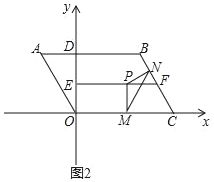
查看答案和解析>>【题目】如图1,已知平行四边形ABCO,以点O为原点,OC所在的直线为x轴,建立直角坐标系,AB交y轴于点D,AD=2,OC=6,∠A=60°,线段EF所在的直线为OD的垂直平分线,点P为线段EF上的动点,PM⊥x轴于点M点,点E与E′关于x轴对称,连接BP、E′M.
(1)请直接写出点A的坐标为_____,点B的坐标为_____;
(2)当BP+PM+ME′的长度最小时,请直接写出此时点P的坐标为_____;
(3)如图2,点N为线段BC上的动点且CM=CN,连接MN,是否存在点P,使△PMN为等腰三角形?若存在,请求出所有满足要求的EP的值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】佳佳果品店在批发市场购买某种水果销售,第一次用1200元购进若干千克,并以每千克8元出售,很快售完.由于水果畅销,第二次购买时,每千克的进价比第一次提高了10%,用1452元所购买的数量比第一次多20千克,以每千克9元售出100千克后,因出现高温天气,水果不易保鲜,为减少损失,便降价50%售完剩余的水果.
(1)求第一次水果的进价是每千克多少元?
(2)该果品店在这两次销售中,总体上是盈利还是亏损?盈利或亏损了多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知MN是⊙O的直径,直线PQ与⊙O相切于P点,NP平分∠MNQ.

(1)求证:NQ⊥PQ;
(2)若⊙O的半径R=2,NP= ,求NQ的长.
,求NQ的长.
相关试题

