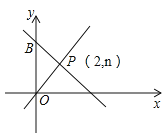
【题目】如图,一次函数y=-x+m的图象与x轴和y轴分别交于点A和点B,与正比例函数![]() 图象交于点P(2,n).
图象交于点P(2,n).
(1)求m和n的值;
(2)求△POB的面积;
(3)在直线OP上是否存在异与点P的另一点C,使得△OBC与△OBP的面积相等?若存在,请求出C点的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)m的值为5,n的值为3.(2)5;(3)点C的坐标为(﹣2,﹣3).
【解析】试题(1)先把P(2,n)代入y=![]() x即可得到n的值,从而得到P点坐标为(2,3),然后把P点坐标代入y=-x+m可计算出m的值;
x即可得到n的值,从而得到P点坐标为(2,3),然后把P点坐标代入y=-x+m可计算出m的值;
(2)先利用一次函数解析式确定B点坐标,然后根据三角形面积公式求解即可;
(3)根据△OBC与△OBP有一条公共边,可知点C横坐标的绝对值与点P横坐标的绝对值相等,根据题意即可确定出点C的横坐标,代入解析式即可得到点C的坐标.
试题解析:(1)∵点P(2,n)在正比例函数y=![]() x图象上,
x图象上,
∴n=![]() ×2=3,
×2=3,
∴点P的坐标为(2,3),
∵点P(2,3)在一次函数y=﹣x+m的图象上,
∴3=﹣2+m,解得:m=5,
∴一次函数解析式为y=﹣x+5,
∴m的值为5,n的值为3;
(2)当x=0时,y=﹣x+5=5,
∴点B的坐标为(0,5),
∴S△POB=![]() OBxP=
OBxP=![]() ×5×2=5;
×5×2=5;
(3)存在,
∵S△OBC=![]() OB|xC|=S△POB=5,
OB|xC|=S△POB=5,
∴xC=﹣2或xC=2(舍去),
当x=﹣2时,y=![]() ×(﹣2)=﹣3,
×(﹣2)=﹣3,
∴点C的坐标为(﹣2,﹣3).
-
科目: 来源: 题型:
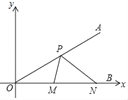
查看答案和解析>>【题目】如图,∠AOB的边OB与x轴正半轴重合,点P是OA上的一动点,点N(6,0)是OB上的一定点,点M是ON的中点,∠AOB=30°,要使PM+PN最小,则点P的坐标为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解答下列问题:
(1)已知一元二次方程ax2+bx+c=0(a≠0)有两根x1 , x2(b2﹣4ac≥0).用求根公式写出x1 , x2 , 并证明x1+x2=﹣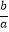 ,x1x 2=
,x1x 2= 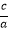
(2)若一元二次方程x2+x﹣1=0的两根为m,n,运用(1)中的结论,求 +
+  的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,折叠长方形(四个角都是直角)的一边AD使点D落在BC边的点F处,已知AB=DC=8cm,AD=BC=10cm,求EC的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】A,B两地相距20km.甲、乙两人都由A地去B地,甲骑自行车,平均速度为10km/h;乙乘汽车,平均速度为40km/h,且比甲晚1.5h出发.设甲的骑行时间为x(h)(0≤x≤2)
(1)根据题意,填写下表:
时间x(h)
与A地的距离
0.5
1.8
_____
甲与A地的距离(km)
5
20
乙与A地的距离(km)
0
12
(2)设甲,乙两人与A地的距离为y1(km)和y2(km),写出y1,y2关于x的函数解析式;
(3)设甲,乙两人之间的距离为y,当y=12时,求x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知P(﹣3,m)和Q(1,m)是抛物线y=2x2+bx+1上的两点.
(1)求b的值;
(2)将抛物线y=2x2+bx+1的图象向上平移k(k是正整数),使平移后的图象的顶点在x轴上,求k的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,一次函数y=﹣2x+8的图象与x轴,y轴分别交于点A,点C,过点A作AB⊥x轴,垂足为点A,过点C作CB⊥y轴,垂足为点C,两条垂线相交于点B.

(1)线段AB,BC,AC的长分别为AB= ,BC= ,AC= ;
(2)折叠图1中的△ABC,使点A与点C重合,再将折叠后的图形展开,折痕DE交AB于点D,交AC于点E,连接CD,如图2.
请从下列A、B两题中任选一题作答,我选择 题.
A:①求线段AD的长;
②在y轴上,是否存在点P,使得△APD为等腰三角形?若存在,请直接写出符合条件的所有点P的坐标;若不存在,请说明理由.
B:①求线段DE的长;
②在坐标平面内,是否存在点P(除点B外),使得以点A,P,C为顶点的三角形与△ABC全等?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
相关试题

